摘要：2．从内容上来看.主要是:①考查直线和平面的各种位置关系的判定和性质.这类试题一般难度不大.多为选择题和填空题,②计算角的问题.试题中常见的是异面直线所成的角.直线与平面所成的角.平面与平面所成的二面角.这类试题有一定的难度和需要一定的解题技巧.通常要把它们转化为相交直线所成的角,③求距离.试题中常见的是点与点之间的距离.点到直线的距离.点到平面的距离.直线与直线的距离.直线到平面的距离.要特别注意解决此类问题的转化方法,④简单的几何体的侧面积和表面积问题.解此类问题除特殊几何体的现成的公式外.还可将侧面展开.转化为求平面图形的面积问题,⑤体积问题.要注意解题技巧.如等积变换.割补思想的应用.⑥三视图.辨认空间几何体的三视图.三视图与表面积.体积内容相结合.
网址：http://m.1010jiajiao.com/timu_id_120752[举报]
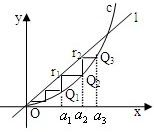设a＞0，如图，已知直线l：y=ax及曲线C：y=x2，C上的点Q1的横坐标为a1（0＜a1＜a）．从C上的点Qn（n≥1）作直线平行于x轴，交直线l于点Pn+1，再从点Pn+1作直线平行于y轴，交曲线C于点Qn+1．Qn（n=1，2，3，…）的横坐标构成数列{an}．（Ⅰ）试求an+1与an的关系，并求{an}的通项公式；
（Ⅱ）当a=1，a1≤
| 1 |
| 2 |
| n |
 |
| k=1 |
| 1 |
| 32 |
（Ⅲ）当a=1时，证明
| n |
|
| k-1 |
| 1 |
| 3 |
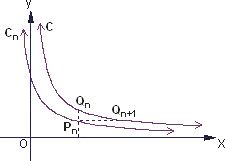如图，已知曲线C：y=| 1 |
| x |
| 1 |
| x+2-n |
（I）求a1，a2，a3的值；
（II）求数列{an}的通项公式；
（III）设△PiQiQi+1（i∈N*）和面积为Si，记f(n)=
| n |
|
| i=1 |
| 1 |
| 6 |