网址:http://m.1010jiajiao.com/timu_id_118231[举报]
| a |
| 1 | ||
|
(2)对于任意给定的a≥2,由(1)所确定的y解集(用区间表示)记为I(a),我们规定:区间[m,n]的长度为n-m.如果I(a)的长度为r(a),试求当a取什么值时,r(a)取得最小值,并求r(a)的最小值及此时的I(a).
(2009•普宁市模拟)为了确保神州七号飞船发射时的信息安全,信息须加密传输,发送方由明文→密文(加密),接受方由密文→明文(解密),已知加密的方法是:密码把英文的明文(真实文)按字母分解,其中英文的a,b,c,…,z的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数(见下表):
|
(本小题满分12分)
如图,在边长为4的菱形 中,
中, .点
.点 分别在边
分别在边 上,点
上,点 与点
与点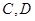 不重合,
不重合, ,
, .沿
.沿 将
将 翻折到
翻折到 的位置,使平面
的位置,使平面 ⊥平面
⊥平面 .
.

(1)求证: ⊥平面
⊥平面 ;
;
(2)当 取得最小值时,请解答以下问题:
取得最小值时,请解答以下问题:
(i)求四棱锥 的体积;
的体积;
(ii)若点 满足
满足 =
=
 (
( ),试探究:直线
),试探究:直线 与平面
与平面 所成角的大小是否一定大于
所成角的大小是否一定大于 ?并说明理由.
?并说明理由.
查看习题详情和答案>>
(本小题满分14分)
 Monte-Carlo方法在解决数学问题中有广泛的应用。下面是利用Monte-Carlo方法来计算定积分。考虑定积分
Monte-Carlo方法在解决数学问题中有广泛的应用。下面是利用Monte-Carlo方法来计算定积分。考虑定积分![]() ,这时
,这时![]() 等于由曲线
等于由曲线![]() ,
,![]() 轴,
轴,![]() 所围成的区域M的面积,为求它的值,我们在M外作一个边长为1正方形OABC。设想在正方形OABC内随机投掷
所围成的区域M的面积,为求它的值,我们在M外作一个边长为1正方形OABC。设想在正方形OABC内随机投掷![]() 个点,若
个点,若![]() 个点中有
个点中有![]() 个点落入
个点落入![]() 中,则
中,则![]() 的面积的估计值为
的面积的估计值为![]() ,此即为定积分
,此即为定积分![]() 的估计值I。向正方形
的估计值I。向正方形![]() 中随机投掷10000个点,有
中随机投掷10000个点,有![]() 个点落入区域M
个点落入区域M
(1)若![]() =2099,计算I的值,并以实际值比较误差是否在5%以内
=2099,计算I的值,并以实际值比较误差是否在5%以内
(2)求![]() 的数学期望
的数学期望
(3)用以上方法求定积分,求I与实际值之差在区间(—0.01,0.01)的概率
附表:![]()
| n | 1899 | 1900 | 1901 | 2099 | 2100 | 2101 |
| P(n) | 0.0058 | 0.0062 | 0.0067 | 0.9933 | 0.9938 | 0.9942 |
(本小题满分14分)
 Monte-Carlo方法在解决数学问题中有广泛的应用。下面是利用Monte-Carlo方法来计算定积分。考虑定积分
Monte-Carlo方法在解决数学问题中有广泛的应用。下面是利用Monte-Carlo方法来计算定积分。考虑定积分![]() ,这时
,这时![]() 等于由曲线
等于由曲线![]() ,
,![]() 轴,
轴,![]() 所围成的区域M的面积,为求它的值,我们在M外作一个边长为1正方形OABC。设想在正方形OABC内随机投掷
所围成的区域M的面积,为求它的值,我们在M外作一个边长为1正方形OABC。设想在正方形OABC内随机投掷![]() 个点,若
个点,若![]() 个点中有
个点中有![]() 个点落入
个点落入![]() 中,则
中,则![]() 的面积的估计值为
的面积的估计值为![]() ,此即为定积分
,此即为定积分![]() 的估计值I。向正方形
的估计值I。向正方形![]() 中随机投掷10000个点,有
中随机投掷10000个点,有![]() 个点落入区域M
个点落入区域M
(1)若![]() =2099,计算I的值,并以实际值比较误差是否在5%以内
=2099,计算I的值,并以实际值比较误差是否在5%以内
(2)求![]() 的数学期望
的数学期望
(3)用以上方法求定积分,求I与实际值之差在区间(—0.01,0.01)的概率
附表:![]()
| n | 1899 | 1900 | 1901 | 2099 | 2100 | 2101 |
| P(n) | 0.0058 | 0.0062 | 0.0067 | 0.9933 | 0.9938 | 0.9942 |