题目内容
(本小题满分12分)
如图,在边长为4的菱形 中,
中, .点
.点 分别在边
分别在边 上,点
上,点 与点
与点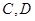 不重合,
不重合, ,
, .沿
.沿 将
将 翻折到
翻折到 的位置,使平面
的位置,使平面 ⊥平面
⊥平面 .
.

(1)求证: ⊥平面
⊥平面 ;
;
(2)当 取得最小值时,请解答以下问题:
取得最小值时,请解答以下问题:
(i)求四棱锥 的体积;
的体积;
(ii)若点 满足
满足 =
=
 (
( ),试探究:直线
),试探究:直线 与平面
与平面 所成角的大小是否一定大于
所成角的大小是否一定大于 ?并说明理由.
?并说明理由.
(1)∵ 菱形 的对角线互相垂直,∴
的对角线互相垂直,∴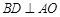 ,
,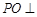 平面
平面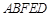 ,∴
,∴ 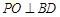 ,∵
,∵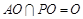 ,∴
,∴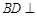 平面
平面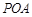 (2)(i)3 (ii) 一定大于
(2)(i)3 (ii) 一定大于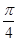 ,用向量可以求出
,用向量可以求出
【解析】
试题分析:(1)证明:∵ 菱形 的对角线互相垂直,
的对角线互相垂直,
∴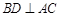 ,∴
,∴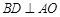 ,
……1分
,
……1分
∵ 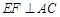 ,∴
,∴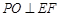 .
.
∵ 平面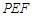 ⊥平面
⊥平面 ,平面
,平面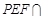 平面
平面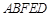
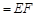 ,且
,且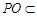 平面
平面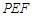 ,
,
∴ 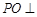 平面
平面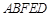 ,
,
∵ 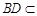 平面
平面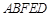 ,∴
,∴ 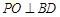 .
……3分
.
……3分
∵ 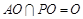 ,∴
,∴ 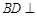 平面
平面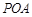 . ……4分
. ……4分
(2)如图,以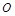 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系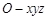 .
……5分
.
……5分
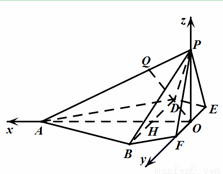
(ⅰ)设 因为
因为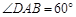 ,所以
,所以 为等边三角形,
为等边三角形,
故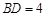 ,
,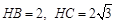 .又设
.又设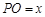 ,则
,则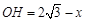 ,
,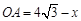 .
.
所以 ,
,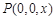 ,
,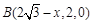 ,
,
故 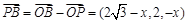 ,
……6分
,
……6分
所以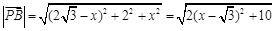 ,
,
当 时,
时,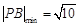 . 此时
. 此时 ,
,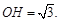 ……7分
……7分
由(1)知,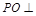 平面
平面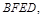
所以 .
……8分
.
……8分
(ⅱ)设点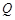 的坐标为
的坐标为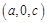 ,
,
由(i)知,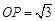 ,则
,则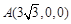 ,
,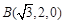 ,
, ,
,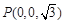 .
.
所以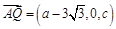 ,
, ,
……9分
,
……9分
∵ ,
,
∴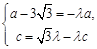
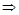
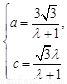 .
.
∴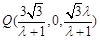 ,
,
∴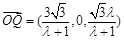 .
……10分
.
……10分
设平面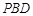 的法向量为
的法向量为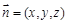 ,则
,则 .
.
∵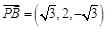 ,
,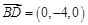 ,∴
,∴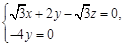 ,
,
取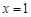 ,解得:
,解得: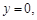
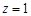 , 所以
, 所以 .
……11分
.
……11分
设直线 与平面
与平面 所成的角
所成的角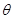 ,
,
∴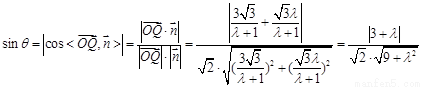
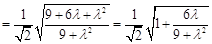 .
……12分
.
……12分
又∵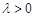 ∴
∴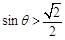 .
……13分
.
……13分
∵ ,∴
,∴ .
.
因此直线 与平面
与平面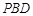 所成的角大于
所成的角大于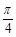 ,即结论成立.
……14分
,即结论成立.
……14分
考点:本小题主要考查线面垂直的证明和用空间向量解决立体几何问题,考查学生的空间想象能力和运算求解能力.
点评:用传统的方法证明立体几何问题时要紧扣定理,定理中要求的条件缺一不可;用空间向量解决立体几何问题时问题变得简单,但是运算量比较大,要仔细运算,以防出错.
