摘要：(3) 若表示数表中第n行第i个数.试用表示第n+1行中由所生成的数．
网址：http://m.1010jiajiao.com/timu_id_11761[举报]
（2006•静安区二模）一个数表如图所示：
对于任意的正整数n，表中第n+1行中的数均由第n行中的数按相同规律生成得到．设Kn表示位于第n行的数的个数，Sn表示第n行各数的和．
（1）试求K6、S6；
（2）求Sn；
（3）若ani表示数表中第n行第i个数，试用ani表示第n+1行中由ani所生成的数（写出它们之间的关系式）．
查看习题详情和答案>>
对于任意的正整数n，表中第n+1行中的数均由第n行中的数按相同规律生成得到．设Kn表示位于第n行的数的个数，Sn表示第n行各数的和．
（1）试求K6、S6；
（2）求Sn；
（3）若ani表示数表中第n行第i个数，试用ani表示第n+1行中由ani所生成的数（写出它们之间的关系式）．
我们用部分自然数构造如下的数表：用aij(i≤j)表示第i行第j个数(i、j为正整数)，使aij＝aii＝i；每行中的其余各数分别等于其“肩膀”上的两个数之和(第一、二行除外，如图)，设第n(n为正整数)行中各数之和为B．
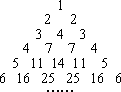
(Ⅰ)试写出b2－2b1，b3－2b2，b4－2b3，b5－2b4，并推测bn+1和bn的关系(无需证明)；
(Ⅱ)证明数列{bn＋2}是等比数列，并求数列{bn}的通项公式bn；
(Ⅲ)数列{bn}中是否存在不同的三项bp，bq，br(p，q，r为正整数)恰好成等差数列？若存在求出p，q，r的关系；若不存在，请说明理由．
原创）重庆市第一中学校高2014级半期考试后，某文科班数学老师抽取10名同学的数学成绩对该科进行抽样分析，得到第i个同学每天花在数学上的学习时间xi（单位：小时）与数学考试成绩yi（单位：百分）的数据资料，算得
xi=15，
yi=10，
xiyi=15.695，
xi2=24.08
（Ⅰ）求数学考试成绩y对每天花在数学上的学习时间x的线性回归方程y=bx+a；（a，b 均用分数表示）
（Ⅱ）若某同学每天花在数学上的学习时间为2小时，预测该同学本次考试的成绩，（保留两位小数）．
附：线性回归方程y=bx+a中，b=
，a=
-b
．
查看习题详情和答案>>
| 10 |
 |
| i-1 |
| 10 |
|
| i-1 |
| 10 |
|
| i-1 |
| 10 |
|
| i-1 |
（Ⅰ）求数学考试成绩y对每天花在数学上的学习时间x的线性回归方程y=bx+a；（a，b 均用分数表示）
（Ⅱ）若某同学每天花在数学上的学习时间为2小时，预测该同学本次考试的成绩，（保留两位小数）．
附：线性回归方程y=bx+a中，b=
| |||||||
|
. |
| y |
. |
| x |
把正整数按上小下大、左小右大的原则排成如图所示的数表：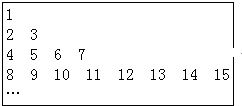
把正整数按上小下大、左小右大的原则排成如图所示的数表：