题目内容
 把正整数按上小下大、左小右大的原则排成如图所示的数表:
把正整数按上小下大、左小右大的原则排成如图所示的数表:设aij(i、j∈N*)是位于这个数表中从上往下数第i行、从左往右数第j个数.数表中第i行共有2i-1个正整数.
(1)若aij=2010,求i、j的值;
(2)记An=a11+a22+a33+…+ann(n∈N*),试比较An与n2+n的大小,并说明理由.
分析:(1)由题目中图中数的排列规律,我们发现图中是把正整数按从小下大、左小右大的原则进行排列,且第i行的第一个数是2i-1,由此不难推断2010的位置.
(2)由(1)的结论,我们易对An=a11+a22+a33+…+ann(n∈N*),进行化简,并写出An与n2+n的前若干项,观察后,可根据归纳推理对An与n2+n的大小进行猜想,然后再用数学归纳法进行证明.
(2)由(1)的结论,我们易对An=a11+a22+a33+…+ann(n∈N*),进行化简,并写出An与n2+n的前若干项,观察后,可根据归纳推理对An与n2+n的大小进行猜想,然后再用数学归纳法进行证明.
解答:解:(1)数表中前n行共有1+2+22++2n-1=2n-1个数,
即第i行的第一个数是2i-1,
∴aij=2i-1+j-1.
∵210<2010<211,aij=2010,
∴i=11.
令210+j-1=2010,
解得j=2010-210+1=987.
(2)∵An=a11+a22+a33+…+ann
=(1+2+22+…+2n-1)+[0+1+2+…+(n-1)]
=2n-1+
∴An-(n2+n)=2n-1+
-(n2+n)=2n-
.
当n=1时,2n<
,则An<n2+n;
当n=2时,2n<
,则An<n2+n;
当n=3时,2n<
,则An<n2+n;
当n≥4时,猜想:2n>
.
下面用数学归纳法证明猜想正确.
①当n=4时,24=16>
,
即2n>
成立;
②假设当n=k(k≥4)时,猜想成立,即2k>
,
则2k+1=2×2k>2×
=k2+3k+2,
∵k2+3k+2-
=
=
>0,
∴2k+1>
.
即当n=k+1时,猜想也正确.
由①、②得当n≥4时,2n>
成立.
当n≥4时,An>n2+n.
综上所述,当n=1,2,3时,An<n2+n;当n≥4时,An>n2+n.
即第i行的第一个数是2i-1,
∴aij=2i-1+j-1.
∵210<2010<211,aij=2010,
∴i=11.
令210+j-1=2010,
解得j=2010-210+1=987.
(2)∵An=a11+a22+a33+…+ann
=(1+2+22+…+2n-1)+[0+1+2+…+(n-1)]
=2n-1+
| n(n-1) |
| 2 |
∴An-(n2+n)=2n-1+
| n(n-1) |
| 2 |
| n2+3n+2 |
| 2 |
当n=1时,2n<
| n2+3n+2 |
| 2 |
当n=2时,2n<
| n2+3n+2 |
| 2 |
当n=3时,2n<
| n2+3n+2 |
| 2 |
当n≥4时,猜想:2n>
| n2+3n+2 |
| 2 |
下面用数学归纳法证明猜想正确.
①当n=4时,24=16>
| 42+3×4+2 |
| 2 |
即2n>
| n2+3n+2 |
| 2 |
②假设当n=k(k≥4)时,猜想成立,即2k>
| k2+3k+2 |
| 2 |
则2k+1=2×2k>2×
| k2+3k+2 |
| 2 |
∵k2+3k+2-
| (k+1)2+3(k+1)+2 |
| 2 |
| 2k2+6k+4-k2-5k-6 |
| 2 |
| (k+2)(k-1) |
| 2 |
∴2k+1>
| (k+1)2+3(k+1)+2 |
| 2 |
即当n=k+1时,猜想也正确.
由①、②得当n≥4时,2n>
| n2+3n+2 |
| 2 |
当n≥4时,An>n2+n.
综上所述,当n=1,2,3时,An<n2+n;当n≥4时,An>n2+n.
点评:数学归纳法常常用来证明一个与自然数集N相关的性质,其步骤为:设P(n)是关于自然数n的命题,若1)(奠基) P(n)在n=1时成立;2)(归纳) 在P(k)(k为任意自然数)成立的假设下可以推出P(k+1)成立,则P(n)对一切自然数n都成立.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a63,54为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a63,54为 把正整数按上小下大、左小右大的原则排成如图所示的数表:
把正整数按上小下大、左小右大的原则排成如图所示的数表: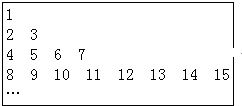 把正整数按上小下大、左小右大的原则排成如图所示的数表:
把正整数按上小下大、左小右大的原则排成如图所示的数表: 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a63,60为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a63,60为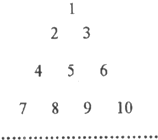 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.若ai,j=2009,则i,j的值分别为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.若ai,j=2009,则i,j的值分别为