摘要: 设函数分别在.处取得极小值.极大值.平面上点A.B的坐标分别为.,该平面上动点P满足,点Q是点P关于直线的对称点.求(Ⅰ)点A.B的坐标 ,(Ⅱ)动点Q的轨迹方程18解: (Ⅰ)令解得当时,, 当时, ,当时,所以,函数在处取得极小值,在取得极大值,故,所以, 点A.B的坐标为.(Ⅱ) 设...所以.又PQ的中点在上.所以消去得
网址:http://m.1010jiajiao.com/timu_id_11472[举报]
(本小题满分14分)设函数![]() ,其图象对应的曲线设为G.(Ⅰ)设
,其图象对应的曲线设为G.(Ⅰ)设![]() 、
、![]() 、
、![]() ,
,![]() 为经过点(2,2)的曲线G的切线,求
为经过点(2,2)的曲线G的切线,求![]() 的方程;
的方程;
(Ⅱ)已知曲线G在点A![]() 、B
、B![]() 处的切线的斜率分别为0、
处的切线的斜率分别为0、![]() ,求证:
,求证:![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,当![]() 时,
时,![]() 恒成立,求常数
恒成立,求常数![]() 的最小值.
的最小值.
(本小题满分14分)
设函数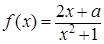 ,函数g(x)=
,函数g(x)= 分别在x=m和x=n处取得极值,且
分别在x=m和x=n处取得极值,且
m<n
(1)求 的值
的值
(2)求证:f(x)在区间[m,n]上是增函数
(3)设f(x)在区间[m,n]上的最大值和最小值分别为M和N,试问当实数a为何值时,M-N取得最小值?并求出这个最小值
查看习题详情和答案>>
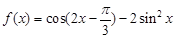 .
.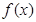 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 求a的值.
求a的值.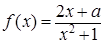 ,函数g(x)=
,函数g(x)=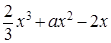 分别在x=m和x=n处取得极值,且
分别在x=m和x=n处取得极值,且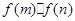 的值
的值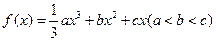 ,其图象对应的曲线设为G.(Ⅰ)设
,其图象对应的曲线设为G.(Ⅰ)设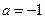 、
、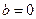 、
、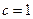 ,
,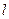 为经过点(2,2)的曲线G的切线,求
为经过点(2,2)的曲线G的切线,求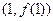 、B
、B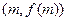 处的切线的斜率分别为0、
处的切线的斜率分别为0、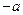 ,求证:
,求证: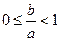 ;
;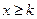 时,
时,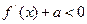 恒成立,求常数
恒成立,求常数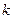 的最小值.
的最小值.