摘要:20.设分别为椭圆的左.右顶点.椭圆长半轴的长等于焦距.且为它的右准线.(Ⅰ).求椭圆的方程,(Ⅱ).设为右准线上不同于点(4.0)的任意一点.若直线分别与椭圆相交于异于的点.证明点在以为直径的圆内.(此题不要求在答题卡上画图)点评:本小题主要考查直线.圆和椭圆等平面解析几何的基础知识.考查综合运用数学知识进行推理运算的能力和解决问题的能力.解:(Ⅰ)依题意得 a=2c.=4.解得a=2.c=1.从而b=.故椭圆的方程为 .得A.设M(x0.y0).∵M点在椭圆上.∴y0=(4-x02). 1又点M异于顶点A.B.∴-2<x0<2.由P.A.M三点共线可以得P(4.).从而=(x0-2.y0).=(2.).∴?=2x0-4+=(x02-4+3y02). 2将1代入2.化简得?=(2-x0).∵2-x0>0.∴?>0.则∠MBP为锐角.从而∠MBN为钝角.故点B在以MN为直径的圆内.解法2:由.设M(x1.y1).N(x2.y2).则-2<x1<2.-2<x2<2.又MN的中点Q的坐标为(.).依题意.计算点B到圆心Q的距离与半径的差-=(-2)2+()2-[(x1-x2)2+(y1-y2)2] =(x1-2) (x2-2)+y1y1 3又直线AP的方程为y=.直线BP的方程为y=.而点两直线AP与BP的交点P在准线x=4上.∴.即y2= 4又点M在椭圆上.则.即 5
网址:http://m.1010jiajiao.com/timu_id_11385[举报]
(本小题满分14分)设![]() 分别是椭圆
分别是椭圆![]() :
:![]() 的左、右焦点.
的左、右焦点.
(1)若椭圆![]() 上的点
上的点![]() 到
到![]() 两点的距离之和为4,试求椭圆
两点的距离之和为4,试求椭圆![]() 的方程和焦点坐标;
的方程和焦点坐标;
(2)设点![]() 是(1)中所得椭圆上的动点,点
是(1)中所得椭圆上的动点,点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最大值.
的最大值.
(本小题满分14分)
设![]() ,椭圆方程为
,椭圆方程为![]() ,抛物线方程为
,抛物线方程为![]() .如图6所示,过点
.如图6所示,过点![]() 作
作![]() 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为![]() ,已知抛物线在点
,已知抛物线在点![]() 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点![]() .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设![]() 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点![]() ,使得
,使得![]() 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).


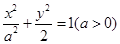 的左、右焦点分别为F1、F2,A是椭圆C上的一点,
的左、右焦点分别为F1、F2,A是椭圆C上的一点,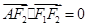 ,坐标原点O到直线AF1的距离为
,坐标原点O到直线AF1的距离为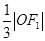 .
.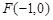 ,交
y 轴于点M,若
,交
y 轴于点M,若 ,求直线l 的斜率.
,求直线l 的斜率.