摘要:C.OP两点间的距离为 D.OP两点间的距离为 2,4,6 A.地球绕太阳运行的周期和地球到太阳中心的距离 B.地球绕太阳运行的周期和地球的半径 C.月球绕地球运行的周期和地球的半径 D.月球绕地球运行的周期和月球到地球中心的距离
网址:http://m.1010jiajiao.com/timu_id_1095071[举报]
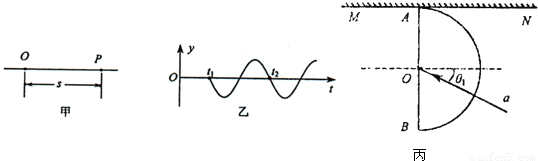
(1)如图甲所示,O点为振源.OP距离为s.t=0时刻,O点从平衡位置开始向下负方向)振动,产生向右沿直线传播的简谐横波,图乙为P点的振动图象(从t1时刻开始振动).则______.(填入正确选项前的字母)
A.该波的频率为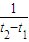
B.t2时刻P点的速度最大,方向沿y正方向
C.这列波的波长为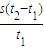
D.若t2时刻O点处于负最大位移处,则s可能是波长的 倍
倍
(2)如图丙所示,半圆形玻璃砖的半径R=10cm,折射率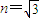 ,直径AB与屏MN垂直并接触于A点,一细束单色光a以入射角θ1=30°沿半径射向玻璃砖的圆心O,在屏MN上出现了两个光斑.求这两个光斑间的距离L.
,直径AB与屏MN垂直并接触于A点,一细束单色光a以入射角θ1=30°沿半径射向玻璃砖的圆心O,在屏MN上出现了两个光斑.求这两个光斑间的距离L.
查看习题详情和答案>>

A.该波的频率为
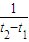
B.t2时刻P点的速度最大,方向沿y正方向
C.这列波的波长为
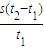
D.若t2时刻O点处于负最大位移处,则s可能是波长的
 倍
倍(2)如图丙所示,半圆形玻璃砖的半径R=10cm,折射率
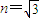 ,直径AB与屏MN垂直并接触于A点,一细束单色光a以入射角θ1=30°沿半径射向玻璃砖的圆心O,在屏MN上出现了两个光斑.求这两个光斑间的距离L.
,直径AB与屏MN垂直并接触于A点,一细束单色光a以入射角θ1=30°沿半径射向玻璃砖的圆心O,在屏MN上出现了两个光斑.求这两个光斑间的距离L.查看习题详情和答案>>
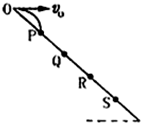 如图所示,斜面上O、P、Q、R、S五个点,距离关系为
如图所示,斜面上O、P、Q、R、S五个点,距离关系为. |
| OP |
. |
| PQ |
. |
| QR |
. |
| RS |
查看习题详情和答案>>
水平放置的两块平行金属板长L=5.0 cm,两板间距d=1.0 cm,两板间电压为90 v,且上板为正,一个电子沿水平方向以速度v0=2.0×107 m/s,从两板中间射入,如图.已知电子的电量为1.6×10-19 C,质量为9.1×10-31 kg求:
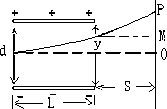
(1)电子偏离金属板时的侧位移是多少?
(2)电子离开电场后,打在屏上的P点,若S=10 cm,求OP的长?
在“验证动量守恒定律”实验中
①下列做法正确的是 。
A.斜槽轨道必须光滑
B.斜槽轨道末端点的切线可以不水平
C.应让入射小球每次从斜槽上相同的位置自由滑下
D.需要的测量工具是天平、刻度尺和游标卡尺
E.重复实验10次后用尽可能小的圆把所有落点圈在里面,其圆心就是各小球落点的平均位置

②如图,O为挂在斜槽边缘的重垂线在白纸上所指的位置,M P、N为两小球实验后得到的落点的平均位置,两小球质量ml、m2且m1>m2。测得OM,OP、ON间的距离分别为Sl、S2、S3,则验证动量守恒定律是否成立的表达式为 (用m1、m2、S1、S2、S3表示)。 查看习题详情和答案>>
①下列做法正确的是 。
A.斜槽轨道必须光滑
B.斜槽轨道末端点的切线可以不水平
C.应让入射小球每次从斜槽上相同的位置自由滑下
D.需要的测量工具是天平、刻度尺和游标卡尺
E.重复实验10次后用尽可能小的圆把所有落点圈在里面,其圆心就是各小球落点的平均位置

②如图,O为挂在斜槽边缘的重垂线在白纸上所指的位置,M P、N为两小球实验后得到的落点的平均位置,两小球质量ml、m2且m1>m2。测得OM,OP、ON间的距离分别为Sl、S2、S3,则验证动量守恒定律是否成立的表达式为 (用m1、m2、S1、S2、S3表示)。 查看习题详情和答案>>
如图1所示,用“碰撞试验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.
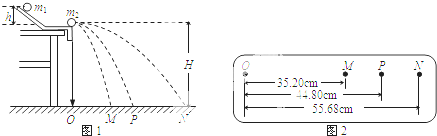
(1)试验中,直接测定小球碰撞前后的速度是不容易的.但是,可以通过仅测量
A.小球开始释放高度h B.小球抛出点距地面得高度H C.小球做平抛运动的射程
(2)图1中O点是小球抛出点在地面上的垂直投影.实验时,先让入射球m1多次从斜轨上S位置静止释放,找到其平均落地点的位置P,测量平抛射程OP.然后,把被碰小球m2静置于轨道的水平部分,再将入射球m1从斜轨上S位置静止释放,与小球m2相碰,并多次重复.接下来要完成的必要步骤是
A.用天平测量两个小球的质量m1、m2
B.测量小球m1开始释放高度h
C.测量抛出点距地面的高度H
D.分别找到m1、m2相碰后平均落地点的位置M、N
E.测量平抛射程OM、ON
(3)若两球相碰前后的动量守恒,其表达式可表示为
(4)经测定,m1=45.0g,m2=7.5g,小球落地点的平均位置距O点的距离如图2所示.碰撞前、后m1-的动量分别为p1与p1′,则p1:p1′=
为
查看习题详情和答案>>

(1)试验中,直接测定小球碰撞前后的速度是不容易的.但是,可以通过仅测量
C
C
(填选项前的序号),间接地解决这个问题.A.小球开始释放高度h B.小球抛出点距地面得高度H C.小球做平抛运动的射程
(2)图1中O点是小球抛出点在地面上的垂直投影.实验时,先让入射球m1多次从斜轨上S位置静止释放,找到其平均落地点的位置P,测量平抛射程OP.然后,把被碰小球m2静置于轨道的水平部分,再将入射球m1从斜轨上S位置静止释放,与小球m2相碰,并多次重复.接下来要完成的必要步骤是
A、D、E
A、D、E
.(填选项前的符号)A.用天平测量两个小球的质量m1、m2
B.测量小球m1开始释放高度h
C.测量抛出点距地面的高度H
D.分别找到m1、m2相碰后平均落地点的位置M、N
E.测量平抛射程OM、ON
(3)若两球相碰前后的动量守恒,其表达式可表示为
m1?OM+m2?ON=m1OP
m1?OM+m2?ON=m1OP
(用②中测量的量表示);若碰撞是弹性碰撞.那么还应满足的表达式为m1?OM2+m2?ON2=m1OP2
m1?OM2+m2?ON2=m1OP2
(用②中测量的量表示).(4)经测定,m1=45.0g,m2=7.5g,小球落地点的平均位置距O点的距离如图2所示.碰撞前、后m1-的动量分别为p1与p1′,则p1:p1′=
14
14
:11;若碰撞结束时m2的动量为p2′,则p1′:p2′=11:2.9
2.9
.实验结果说明,碰撞前、后总动量的比值| P1 | P1′+P2′ |
1.01
1.01
.