题目内容
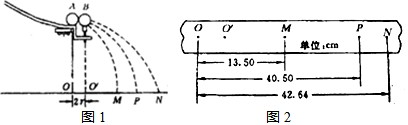
如图1所示,用“碰撞试验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.
(1)试验中,直接测定小球碰撞前后的速度是不容易的.但是,可以通过仅测量
A.小球开始释放高度h B.小球抛出点距地面得高度H C.小球做平抛运动的射程
(2)图1中O点是小球抛出点在地面上的垂直投影.实验时,先让入射球m1多次从斜轨上S位置静止释放,找到其平均落地点的位置P,测量平抛射程OP.然后,把被碰小球m2静置于轨道的水平部分,再将入射球m1从斜轨上S位置静止释放,与小球m2相碰,并多次重复.接下来要完成的必要步骤是
A.用天平测量两个小球的质量m1、m2
B.测量小球m1开始释放高度h
C.测量抛出点距地面的高度H
D.分别找到m1、m2相碰后平均落地点的位置M、N
E.测量平抛射程OM、ON
(3)若两球相碰前后的动量守恒,其表达式可表示为
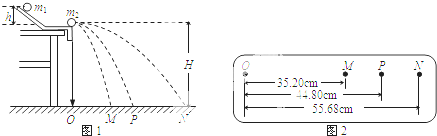
(4)经测定,m1=45.0g,m2=7.5g,小球落地点的平均位置距O点的距离如图2所示.碰撞前、后m1-的动量分别为p1与p1′,则p1:p1′=
为

(1)试验中,直接测定小球碰撞前后的速度是不容易的.但是,可以通过仅测量
C
C
(填选项前的序号),间接地解决这个问题.A.小球开始释放高度h B.小球抛出点距地面得高度H C.小球做平抛运动的射程
(2)图1中O点是小球抛出点在地面上的垂直投影.实验时,先让入射球m1多次从斜轨上S位置静止释放,找到其平均落地点的位置P,测量平抛射程OP.然后,把被碰小球m2静置于轨道的水平部分,再将入射球m1从斜轨上S位置静止释放,与小球m2相碰,并多次重复.接下来要完成的必要步骤是
A、D、E
A、D、E
.(填选项前的符号)A.用天平测量两个小球的质量m1、m2
B.测量小球m1开始释放高度h
C.测量抛出点距地面的高度H
D.分别找到m1、m2相碰后平均落地点的位置M、N
E.测量平抛射程OM、ON
(3)若两球相碰前后的动量守恒,其表达式可表示为
m1?OM+m2?ON=m1OP
m1?OM+m2?ON=m1OP
(用②中测量的量表示);若碰撞是弹性碰撞.那么还应满足的表达式为m1?OM2+m2?ON2=m1OP2
m1?OM2+m2?ON2=m1OP2
(用②中测量的量表示).(4)经测定,m1=45.0g,m2=7.5g,小球落地点的平均位置距O点的距离如图2所示.碰撞前、后m1-的动量分别为p1与p1′,则p1:p1′=
14
14
:11;若碰撞结束时m2的动量为p2′,则p1′:p2′=11:2.9
2.9
.实验结果说明,碰撞前、后总动量的比值| P1 | P1′+P2′ |
1.01
1.01
.分析:验证动量守恒定律实验中,质量可测而瞬时速度较难.因此采用了落地高度不变的情况下,水平射程来反映平抛的初速度大小,所以仅测量小球抛出的水平射程来间接测出速度.过程中小球释放高度不需要,小球抛出高度也不要求.最后可通过质量与水平射程乘积来验证动量是否守恒.
解答:解:(1)验证动量守恒定律实验中,即研究两个小球在轨道水平部分碰撞前后的动量关系,直接测定小球碰撞前后的速度是不容易的,但是通过落地高度不变情况下水平射程来体现速度.故答案是C
(2)实验时,先让入射球ml多次从斜轨上S位置静止释放,找到其平均落地点的位置P,测量平抛射程OP.然后,把被碰小球m2静置于轨道的水平部分,再将入射球ml从斜轨上S位置静止释放,与小球m2相碰,并多次重复.测量平均落点的位置,找到平抛运动的水平位移,因此步骤中D、E是必须的,而且D要在E之前.至于用天平秤质量先后均可以.所以答案是ADE或DEA
(3)设落地时间为t,则v0=
,v1=
,v2=
;
而动量守恒的表达式是m1v0=m1v1+m2v2,
动能守恒的表达式是
m02=
m1v12+
m2v22,
所以若两球相碰前后的动量守恒,则m1?OM+m2?ON=m1?OP成立,
若碰撞是弹性碰撞,动能是守恒的,则有m1?OM2+m2?ON2=m1?OP2成立;
(4)碰撞前后m1动量之比:
=
=
=
,
=
=
=
,
=
=1.01(1~1.01均正确).
故答案为:①C; ②ADE或DEA;③m1?OM+m2?ON=m1OP; m1?OM2+m2?ON2=m1OP2;④14;2.9;1.01.
(2)实验时,先让入射球ml多次从斜轨上S位置静止释放,找到其平均落地点的位置P,测量平抛射程OP.然后,把被碰小球m2静置于轨道的水平部分,再将入射球ml从斜轨上S位置静止释放,与小球m2相碰,并多次重复.测量平均落点的位置,找到平抛运动的水平位移,因此步骤中D、E是必须的,而且D要在E之前.至于用天平秤质量先后均可以.所以答案是ADE或DEA
(3)设落地时间为t,则v0=
| OP |
| t |
| OM |
| t |
| ON |
| t |
而动量守恒的表达式是m1v0=m1v1+m2v2,
动能守恒的表达式是
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以若两球相碰前后的动量守恒,则m1?OM+m2?ON=m1?OP成立,
若碰撞是弹性碰撞,动能是守恒的,则有m1?OM2+m2?ON2=m1?OP2成立;
(4)碰撞前后m1动量之比:
| P1 |
| P1′ |
| OP |
| OM |
| 44.8 |
| 35.2 |
| 14 |
| 11 |
| P1′ |
| P2′ |
| m1×OM |
| m2×ON |
| 45.0×35.2 |
| 7.5×55.68 |
| 11 |
| 2.9 |
| P1 |
| P1′+P2′ |
| m1×OP |
| m1×OM+m2×ON |
故答案为:①C; ②ADE或DEA;③m1?OM+m2?ON=m1OP; m1?OM2+m2?ON2=m1OP2;④14;2.9;1.01.
点评:验证动量守恒定律中,学会在相同高度下,水平射程来间接测出速度,并利用动能守恒定律来解最大速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目