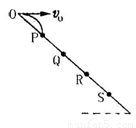
题目内容
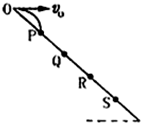如图所示，斜面上O、P、Q、R、S五个点，距离关系为. |
| OP |
. |
| PQ |
. |
| QR |
. |
| RS |
分析：平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动，根据小球竖直位移与水平位移的关系求出时间与初速度的关系，从而进行判断．
解答：解：因为tanθ=
=
=
，解得t=
．
初速度变为原来的2倍，则运动的时间变为原来的2倍，根据x=v0t知，水平位移变为原来的4倍．
因为s=
，知小球落点与抛出点的距离变为原来的4倍．故B正确，A、C、D错误．
故选：B．
| y |
| x |
| ||
| v0t |
| gt |
| 2v0 |
| 2v0tanθ |
| g |
初速度变为原来的2倍，则运动的时间变为原来的2倍，根据x=v0t知，水平位移变为原来的4倍．
因为s=
| x |
| cosθ |
故选：B．
点评：解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，知道小球落在斜面上，竖直位移与水平位移的比值是一定值．
练习册系列答案
相关题目
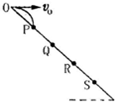如图所示，斜面上O、P、Q、R、S五个点，距离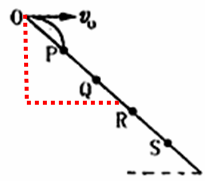
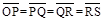，从O点以υ0的初速度水平抛出一个小球，不计空气阻力，小球落在斜面上的P点．若小球从O点以2υ0的初速度水平抛出，则小球将落在斜面上的 （ ）
，从O点以υ0的初速度水平抛出一个小球，不计空气阻力，小球落在斜面上的P点．若小球从O点以2υ0的初速度水平抛出，则小球将落在斜面上的 （ ）