摘要:18.解:(I)的最大值为2..又其图象相邻两对称轴间的距离为2...过点.又∵.(II)解法一:..又的周期为4..解法二:又的周期为4..
网址:http://m.1010jiajiao.com/timu_id_10939[举报]
已知向量
=(sinωx,1),
=(
Acosωx,
cos2ωx)(A>0,ω>0),函数f(x)=
•
的最大值为3,且其图象相邻两条对称轴之间的距离为π.
(I)求函数f(x)的解析式;
(II)将函数y=f(x)的图象向左平移
个单位,再将所得图象上各点的横坐标缩短为原来的
倍,纵坐标不变,得到函数y=g(x)的图象.
(1)求函数g(x)的单调递减区间;
(2)求函数g(x)在[
,
]上的值域.
查看习题详情和答案>>
| m |
| n |
| 3 |
| A |
| 2 |
| m |
| n |
(I)求函数f(x)的解析式;
(II)将函数y=f(x)的图象向左平移
| π |
| 6 |
| 1 |
| 2 |
(1)求函数g(x)的单调递减区间;
(2)求函数g(x)在[
| π |
| 4 |
| π |
| 2 |
已知向量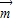 =(sinωx,1),
=(sinωx,1),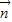 =(
=(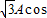 ωx,
ωx,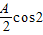 ωx)(A>0,ω>0),函数f(x)=
ωx)(A>0,ω>0),函数f(x)= 的最大值为3,且其图象相邻两条对称轴之间的距离为π.
的最大值为3,且其图象相邻两条对称轴之间的距离为π.
(I)求函数f(x)的解析式;
(II)将函数y=f(x)的图象向左平移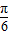 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数y=g(x)的图象.
倍,纵坐标不变,得到函数y=g(x)的图象.
(1)求函数g(x)的单调递减区间;
(2)求函数g(x)在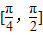 上的值域.
上的值域.
查看习题详情和答案>>
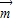 =(sinωx,1),
=(sinωx,1),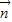 =(
=(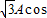 ωx,
ωx,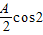 ωx)(A>0,ω>0),函数f(x)=
ωx)(A>0,ω>0),函数f(x)= 的最大值为3,且其图象相邻两条对称轴之间的距离为π.
的最大值为3,且其图象相邻两条对称轴之间的距离为π.(I)求函数f(x)的解析式;
(II)将函数y=f(x)的图象向左平移
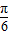 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数y=g(x)的图象.
倍,纵坐标不变,得到函数y=g(x)的图象.(1)求函数g(x)的单调递减区间;
(2)求函数g(x)在
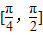 上的值域.
上的值域.查看习题详情和答案>>
已知向量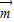 =(sinωx,1),
=(sinωx,1),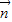 =(
=(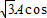 ωx,
ωx,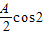 ωx)(A>0,ω>0),函数f(x)=
ωx)(A>0,ω>0),函数f(x)=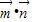 的最大值为3,且其图象相邻两条对称轴之间的距离为π.
的最大值为3,且其图象相邻两条对称轴之间的距离为π.
(I)求函数f(x)的解析式;
(II)将函数y=f(x)的图象向左平移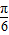 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数y=g(x)的图象.
倍,纵坐标不变,得到函数y=g(x)的图象.
(1)求函数g(x)的单调递减区间;
(2)求函数g(x)在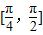 上的值域.
上的值域.
查看习题详情和答案>>
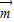 =(sinωx,1),
=(sinωx,1),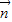 =(
=(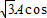 ωx,
ωx,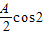 ωx)(A>0,ω>0),函数f(x)=
ωx)(A>0,ω>0),函数f(x)=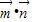 的最大值为3,且其图象相邻两条对称轴之间的距离为π.
的最大值为3,且其图象相邻两条对称轴之间的距离为π.(I)求函数f(x)的解析式;
(II)将函数y=f(x)的图象向左平移
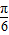 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数y=g(x)的图象.
倍,纵坐标不变,得到函数y=g(x)的图象.(1)求函数g(x)的单调递减区间;
(2)求函数g(x)在
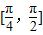 上的值域.
上的值域.查看习题详情和答案>>
 =(sinωx,1),
=(sinωx,1), =(
=(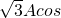 ωx,
ωx,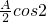 ωx)(A>0,ω>0),函数f(x)=
ωx)(A>0,ω>0),函数f(x)= 的最大值为3,且其图象相邻两条对称轴之间的距离为π.
的最大值为3,且其图象相邻两条对称轴之间的距离为π. 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数y=g(x)的图象.
倍,纵坐标不变,得到函数y=g(x)的图象.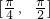 上的值域.
上的值域.