摘要：(3)若已知当地的重力加速度值.则利用本装置可以验证机械能守恒定律．设重物的质量为m=0．5kg.利用(2)的数据求出从开始运动到打下F点的过程中.重物重力势能的减少量△Ep= J.动能的增加量△Ek= J(以上两空均要求保留3位有效数字)．造成两者不相等的主要原因是?
网址：http://m.1010jiajiao.com/timu_id_1087410[举报]
在“利用单摆测重力加速度”的实验中：
（1）已知单摆小球的质量为m，摆长为l，某地重力加速度为g，当单摆做摆角不超过5°的振动时，通过证明可以得到回复力F＝－kx，其中k＝_______。
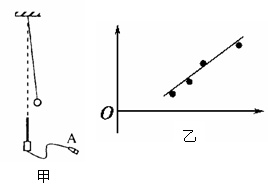
（2）某同学尝试用DIS测量周期。如图甲所示，用一个磁性小球代替原先的摆球，在单摆下方放置一个磁传感器，其轴线恰好位于单摆悬挂点正下方。使单摆做小角度摆动，当磁感应强度测量值最大时，磁性小球位于最低点。若测得连续N个磁感应强度最大值之间的时间间隔为t，则单摆周期的测量值为____________（地磁场和磁传感器的影响可忽略）。
（3）经理论推导可知，单摆在任意摆角θ时的周期公式可近似为T＝T0（1＋
sin2
），式中T0为当摆角θ趋近于0°时的周期。为了用图象法验证该关系式，若某同学在实验中得到了如图乙所示的图线，则图线的斜率为________，纵轴截距为__________。
某同学在用单摆测定重力加速度的实验中，测量5种不同摆长情况下单摆的振动周期，记录结果见下表：
（1）以L为横坐标，T2为纵坐标，作出T2-L图线（如图1），并利用此图线求出重力加速度g=
（2）若某同学测定的g的数值比当地公认值大，造成的原因可能是
A、摆球质量太大了；
B、摆长太长了；
C、摆角太大了（摆角仍小于10°）；
C、量摆长时从悬点量到球的最下端；
D、计算摆长时忘记把小球半径加进去；
E、摆球不是在竖直平面内做简谐振动，而是做圆锥摆运动；
F、计算周期时，将（n-1）次全振动误记为n次全振动；
（3）若某同学根据实验数据作出的图象如图2所示．则造成图象不过坐标原点的原因是
（4）如果已知摆球直径为2.00cm，让刻度尺的零点对准摆线的悬点，摆线竖直下垂．如图①所示，那么单摆摆长是
查看习题详情和答案>>
| L/m | 0.5 | 0.8 | 0.9 | 1.0 | 1.2 |
| T/s | 1.42 | 1.79 | 1.90 | 2.00 | 2.20 |
| T2/s2 | 2.02 | 3.20 | 3.61 | 4.00 | 4.84 |
9.87
9.87
m/s2．（取π2=9.87）?（2）若某同学测定的g的数值比当地公认值大，造成的原因可能是
CEF
CEF
；A、摆球质量太大了；
B、摆长太长了；
C、摆角太大了（摆角仍小于10°）；
C、量摆长时从悬点量到球的最下端；
D、计算摆长时忘记把小球半径加进去；
E、摆球不是在竖直平面内做简谐振动，而是做圆锥摆运动；
F、计算周期时，将（n-1）次全振动误记为n次全振动；
（3）若某同学根据实验数据作出的图象如图2所示．则造成图象不过坐标原点的原因是
漏测小球的半径r
漏测小球的半径r
；?（4）如果已知摆球直径为2.00cm，让刻度尺的零点对准摆线的悬点，摆线竖直下垂．如图①所示，那么单摆摆长是
0.8740
0.8740
m．如果测定了40次全振动所用时间如图②中秒表所示，单摆的运动周期是1.88
1.88
s．
（2013?普陀区二模）在“利用单摆测重力加速度”的实验中：（1）已知单摆小球的质量为m，摆长为l，某地重力加速度为g，当单摆做摆角不超过5°的振动时，通过证明可以得到回复力F=-kx，其中k=
| mg |
| l |
| mg |
| l |
（2）某同学尝试用DIS测量周期．如图甲所示，用一个磁性小球代替原先的摆球，在单摆下方放置一个磁传感器，其轴线恰好位于单摆悬挂点正下方．使单摆做小角度摆动，当磁感应强度测量值最大时，磁性小球位于最低点．若测得连续N个磁感应强度最大值之间的时间间隔为t，则单摆周期的测量值为
| 2t |
| N-1 |
| 2t |
| N-1 |
（3）经理论推导可知，单摆在任意摆角θ时的周期公式可近似为T=T0（1+
| 1 |
| 4 |
| θ |
| 2 |
| 4 |
| T0 |
| 4 |
| T0 |
-4
-4
．
)假设我们已经进入了航天时代，某高中学生组成的航天兴趣小组乘外星科学考察飞船到达了X星球(已知该星球与地球极其相似)，他们准备利用单摆的知识测量X星球表面的重力加速度gx。由于没有规则的小球，他们用了一个不规则的物体代替摆球做成单摆，第一次实验使摆线长为l1，测出周期为T1；第二次实验使摆线长为l2，测出周期为T2。若两次实验中摆线都系在物体的同一位置，则利用这两组数据可测得当地重力加速度的值为gx==____________________。
如果在处理数据时，将摆线长作为摆长，根据T==2π
分别求出两次的g值，然后取其算术平均值作为测得的gx值，则测出的gx值将_________。(填“偏小”或“偏大”)
查看习题详情和答案>>
如果在处理数据时，将摆线长作为摆长，根据T==2π
分别求出两次的g值，然后取其算术平均值作为测得的gx值，则测出的gx值将_________。(填“偏小”或“偏大”)
查看习题详情和答案>>
如图，P、Q为某地区水平地面上的两点，在P点正下方一球形区域内储藏有石油。假定区域周围岩石均匀分布，密度为ρ;石油密度远小于ρ，可将上述球形区域视为空腔。如果没有这一空腔，则该地区重力加速度（正常值）沿竖直方向；当存在空腔时，该地区重力加速度的大小和方向会与正常情况有微小偏离。重力加速度在原竖直方向（即PO方向）上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量，常利用P点附近重力加速度反常现象。已知引力常数为G。
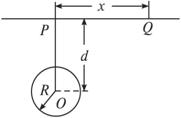
（1）设球形空腔体积为V，球心深度为d（远小于地球半径），
，求空腔所引起的Q点处的重力加速度反常。
（2）若在水平地面上半径为L的范围内发现：重力加速度反常值在δ与kδ(k＞1)之间变化,且重力加速度反常的最大值出现在半径为L的范围的中心。如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
查看习题详情和答案>>