如图所示，水平放置的光滑导轨MN、PQ足够长，两导轨放于竖直向上的匀强磁场中．长为L的导体AB和CD分别以速度v₁和v₂向左、右两个方向匀速运动，关于ABCDA电路中的感应电动势的计算和感应电流方向的判断，下列说法中正确的是（　　）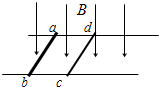

如图所示，水平面上固定有平行导轨，磁感应强度为B的匀强磁场方向竖直向下．同种合金做的导体棒ab、cd横截面积之比为2：1，长度和导轨的宽均为L，ab的质量为m，电阻为r，开始时ab、cd都垂直于导轨静止，不计摩擦．给ab一个向右的瞬时冲量I，在以后的运动中，cd的最大速度V_m、最大加速度a_m、产生的电热各是多少？

如图甲所示，ab、cd为两根放置在同一水平面内且相互平行的金属轨道，相距L，右端连接一个阻值为R的定值电阻，轨道上放有一根导体棒MN，垂直两轨道且与两轨道接触良好，导体棒MN及轨道的电阻均可忽略不计，整个装置处于方向竖直向下的匀强磁场中，磁感应强度大小为B．导体棒MN在外力作用下以图中虚线所示范围的中心位置为平衡位置做简谐运动，振动周期为T，振幅为A，在t=0时刻恰好通过平衡位置，速度大小为v₀，其简谐运动的速度V随时间t按余弦规律变化，如图所示，则下列说法正确的是（　　）

如图所示，“×”型光滑金属导轨abcd固定在绝缘水平面上，ab和cd足够长，∠aOc=60°．虚线MN与∠bOd的平分线垂直，O点到MN的距离为L．MN左侧是磁感应强度大小为B、方向竖直向下的匀强磁场．一轻弹簧右端固定，其轴线与∠bOd的平分线重合，自然伸长时左端恰在O点．一质量为m的导体棒ef平行于MN置于导轨上，导体棒与导轨接触良好．某时刻使导体棒从MN的右侧

L

4

处由静止开始释放，导体在被压缩弹簧的作用下向左运动，当导体棒运动到O点时弹簧与导体棒分离．导体棒由MN运动到O点的过程中做匀速直线运动．导体棒始终与MN平行．已知导体棒与弹簧彼此绝缘，导体棒和导轨单位长度的电阻均为r₀，弹簧被压缩后所获得的弹性势能可用公式EP=

1

2

kx2计算，k为弹簧的劲度系数，x为弹簧的形变量．
（1）证明：导体棒在磁场中做匀速直线运动的过程中，感应电流的大小保持不变；
（2）求弹簧的劲度系数k和导体棒在磁场中做匀速直线运动时速度v₀的大小；
（3）求导体棒最终静止时的位置距O点的距离．

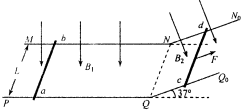如图所示，两条光滑的金属导轨相距L=lm，其中MN段平行于PQ段，位于同一水平面内，NN₀段与QQ₀段平行，位于与水平面成倾角37°的斜面内，且MNN₀与PQQ₀均在竖直平面内．在水平导轨区域和倾斜导轨区域内分别有垂直于水平面和斜面的匀强磁场B₁和B₂，且B₁=B₂=0.5T．ab和cd是质量均为m=0.1kg、电阻均为R=4Ω的两根金属棒，ab置于水平导轨上，ab置于倾斜导轨上，均与导轨垂直且接触良好．从t=0时刻起，ab棒在外力作用下由静止开始沿水平方向向右运动（ab棒始终在水平导轨上运动，且垂直于水平导轨），cd受到F=0.6-0.25t（N）沿斜面向上的力的作用，始终处于静止状态．不计导轨的电阻．（sin37°=0.6）
（1）求流过cd棒的电流强度I_cd随时间t变化的函数关系：
（2）求ab棒在水平导轨上运动的速度v_ab随时间t变化的函数关系；
（3）求从t=0时刻起，1.0s内通过ab棒的电荷量q；
（4）若t=0时刻起，l.0s内作用在ab棒上的外力做功为W=16J，求这段时间内cd棒产生的焦耳热Q_cd．