题目内容
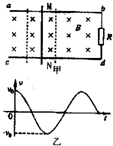 如图甲所示,ab、cd为两根放置在同一水平面内且相互平行的金属轨道,相距L,右端连接一个阻值为R的定值电阻,轨道上放有一根导体棒MN,垂直两轨道且与两轨道接触良好,导体棒MN及轨道的电阻均可忽略不计,整个装置处于方向竖直向下的匀强磁场中,磁感应强度大小为B.导体棒MN在外力作用下以图中虚线所示范围的中心位置为平衡位置做简谐运动,振动周期为T,振幅为A,在t=0时刻恰好通过平衡位置,速度大小为v0,其简谐运动的速度V随时间t按余弦规律变化,如图所示,则下列说法正确的是( )
如图甲所示,ab、cd为两根放置在同一水平面内且相互平行的金属轨道,相距L,右端连接一个阻值为R的定值电阻,轨道上放有一根导体棒MN,垂直两轨道且与两轨道接触良好,导体棒MN及轨道的电阻均可忽略不计,整个装置处于方向竖直向下的匀强磁场中,磁感应强度大小为B.导体棒MN在外力作用下以图中虚线所示范围的中心位置为平衡位置做简谐运动,振动周期为T,振幅为A,在t=0时刻恰好通过平衡位置,速度大小为v0,其简谐运动的速度V随时间t按余弦规律变化,如图所示,则下列说法正确的是( )分析:导体棒MN做简谐运动,写出速度随时间的表达式,根据感应电动势公式确定回路中电动势的瞬时值表达式.由有效值求出电功率.由平均值求出电量.
解答:解:A、导体棒速度的表达式v=v0cos
t,回路中电动势的瞬时值e=BLv=BLv0cos
t,故A错误.
B、电动势有效值E=
Em=
BLv0,导体棒MN中产生交流电的电功率P=
=
,故B正确.
C、电流有效值I=
=
故C正确.
D、电量q=
=
,不能用q=
?
T=
?
T=
,不能用
=
,因为电流随时间是非线性变化的.故D错误
故选BC
| 2π |
| T |
| 2π |
| T |
B、电动势有效值E=
| ||
| 2 |
| ||
| 2 |
| E2 |
| R |
B2L2
| ||
| 2R |
C、电流有效值I=
| E |
| R |
| ||
| 2R |
D、电量q=
| △Φ |
| R |
| BLA |
| R |
. |
| I |
| 1 |
| 4 |
| Im+0 |
| 2 |
| 1 |
| 4 |
| BLv0 |
| 8R |
. |
| I |
| Im+0 |
| 2 |
故选BC
点评:本题提供了产生正弦式交变电流的一种方式.交变电流求热量用有效值,求出电量用平均值.

练习册系列答案
相关题目
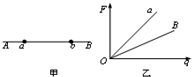 如图甲所示,AB是一个点电荷电场中的一条电场线,图乙中是放在电场线上a、b两点的检验电荷所受电场力与其电量的函数图线,由此可知( )
如图甲所示,AB是一个点电荷电场中的一条电场线,图乙中是放在电场线上a、b两点的检验电荷所受电场力与其电量的函数图线,由此可知( )



 A<
A<