题目内容
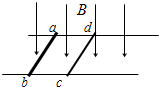 如图所示,水平面上固定有平行导轨,磁感应强度为B的匀强磁场方向竖直向下.同种合金做的导体棒ab、cd横截面积之比为2:1,长度和导轨的宽均为L,ab的质量为m,电阻为r,开始时ab、cd都垂直于导轨静止,不计摩擦.给ab一个向右的瞬时冲量I,在以后的运动中,cd的最大速度Vm、最大加速度am、产生的电热各是多少?
如图所示,水平面上固定有平行导轨,磁感应强度为B的匀强磁场方向竖直向下.同种合金做的导体棒ab、cd横截面积之比为2:1,长度和导轨的宽均为L,ab的质量为m,电阻为r,开始时ab、cd都垂直于导轨静止,不计摩擦.给ab一个向右的瞬时冲量I,在以后的运动中,cd的最大速度Vm、最大加速度am、产生的电热各是多少?分析:首先分析两棒的受力情况,来判断它们的运动情况:给ab冲量后,ab获得速度向右运动,回路中产生感应电流,cd受安培力作用而加速,ab受安培力而减速,当两者速度相等时,都开始做匀速运动,所以开始时cd的加速度最大,最终cd的速度最大,全过程系统动能的损失都转化为电能,电能又转化为内能,先根据电阻定律求出两棒的电阻之比,得到它们产生的热量之比.
根据系统的动量守恒求出最大速度vm.
根据法拉第定律、欧姆定律和安培力公式求出cd的最大加速度am.
根据能量守恒求出产生的电热.
根据系统的动量守恒求出最大速度vm.
根据法拉第定律、欧姆定律和安培力公式求出cd的最大加速度am.
根据能量守恒求出产生的电热.
解答:解:给ab冲量后,ab获得速度向右运动,回路中产生感应电流,cd受安培力作用而加速,ab受安培力而减速,当两者速度相等时,都开始做匀速运动,所以开始时cd的加速度最大,最终cd的速度最大,全过程系统动能的损失都转化为电能,电能又转化为内能.
由于ab、cd横截面积之比为2:1,材料和长度相同,所以根据电阻定律得知,它们的电阻之比为1:2,质量之比为2:1.所以cd棒的质量为
m.
由题,由动量定理得:ab的初速度为v1=
,两棒组成的系统所受的合外力为0,动量守恒,则有:
mv1=(m+
m)vm
解得,最后的共同速度为:vm=
,
开始运动时又有:E=BLv1,I=
,F=BIL,am=
=
,解得:am=
.
据焦耳定律得知:Q=I2Rt∝R,所以cd上产生的电热应该是回路中产生的全部电热的
.
系统统动能的损失为:△Ek=
m
-
(m+
m)
=
,
由能量守恒定律可知,系统产生的电热总量为:Q=△Ek=
,
其中cd上产生电热Qcd=
Q=
.
答:在以后的运动中,cd的最大速度Vm、最大加速度am、产生的电热各是
,
,
.
由于ab、cd横截面积之比为2:1,材料和长度相同,所以根据电阻定律得知,它们的电阻之比为1:2,质量之比为2:1.所以cd棒的质量为
| 1 |
| 2 |
由题,由动量定理得:ab的初速度为v1=
| I |
| m |
mv1=(m+
| 1 |
| 2 |
解得,最后的共同速度为:vm=
| 2I |
| 3m |
开始运动时又有:E=BLv1,I=
| E |
| r+2r |
| F | ||
|
| 2F |
| m |
| 2B2L2I |
| 3m2r |
据焦耳定律得知:Q=I2Rt∝R,所以cd上产生的电热应该是回路中产生的全部电热的
| 2 |
| 3 |
系统统动能的损失为:△Ek=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 m |
| I2 |
| 6m |
由能量守恒定律可知,系统产生的电热总量为:Q=△Ek=
| I2 |
| 6m |
其中cd上产生电热Qcd=
| 2 |
| 3 |
| I2 |
| 9m |
答:在以后的运动中,cd的最大速度Vm、最大加速度am、产生的电热各是
| 2I |
| 3m |
| 2F |
| m |
| I2 |
| 9m |
点评:本题以双杆模型,分析两棒的运动情况是解题至关重要的步骤,再根据电磁感应和力学的规律求解.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 如图所示,两块固连在一起的物块a和b,质量分别是ma和mb.放在水平光滑桌面上,现同时施给他们方向如图所示的推力Fa和拉力Fb,已知Fa>Fb,则a对b的作用力( )
如图所示,两块固连在一起的物块a和b,质量分别是ma和mb.放在水平光滑桌面上,现同时施给他们方向如图所示的推力Fa和拉力Fb,已知Fa>Fb,则a对b的作用力( )



