摘要:736
网址:http://m.1010jiajiao.com/timu_id_1081017[举报]
在利用单摆测重力加速度的实验中某同学测得数据如下:
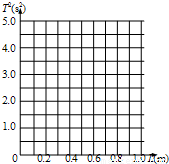
(1)求出周期平方填入表格中(保留小数点最后一位),并在L-T2图上画出图象;
(2)利用图象求出当地重力加速度g=______m/s2.(取π=3.14,计算结果小数点后保留1位)
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求出周期平方填入表格中(保留小数点最后一位),并在L-T2图上画出图象;
| 摆长L(m) | 0.99 | 0.74 | 0.53 | 0.38 | 0.24 |
| 30次全振动时间t(s) | 60.0 | 51.9 | 43.7 | 36.8 | 29.4 |
| 周期平方T2(s2) |
 查看习题详情和答案>>
查看习题详情和答案>>
匀变速直线运动的物体,中间时刻的瞬时速度等于这段时间内的平均速度,某同学在实验中,给出了从0点开始,每5个点取一个计数点的纸带,其中0、1、2、3、4、5、6都为计数点.测得:s1=1.40cm,s2=1.90cm,s3=2.40cm,s4=2.88cm,s5=3.43cm,s6=3.90cm.
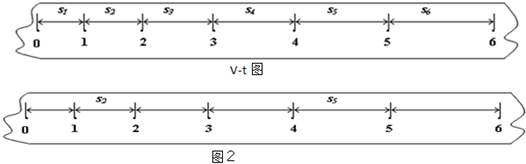
(1)在计时器打出点1、2、3、4、5时,小车的速度分别为:v1=
(2)在求解运动小车的加速度时,两位同学对这一问题有不同看法,甲同学认为,只要在上面计算好的5个速度中,任意取两个,代入公式即可求出加速度,而乙同学则认为,应该选取V-t图象上的相距较远的两个点来计算加速度,你认为哪位同学求解的加速度的方法更合理
(3)在对本纸带的测量中,某同学只测量了如图2两组数据,若每两个相邻计数点间的时间间隔为T,测这个物体运动的加速度为a=
(用S2、S5、T表示).
查看习题详情和答案>>

(1)在计时器打出点1、2、3、4、5时,小车的速度分别为:v1=
16.5
16.5
cm/s,v2=21.5
21.5
cm/s,v3=26.4
26.4
cm/s,v4=31.6cm
31.6cm
cm/s,v5=36.7
36.7
cm/s.(2)在求解运动小车的加速度时,两位同学对这一问题有不同看法,甲同学认为,只要在上面计算好的5个速度中,任意取两个,代入公式即可求出加速度,而乙同学则认为,应该选取V-t图象上的相距较远的两个点来计算加速度,你认为哪位同学求解的加速度的方法更合理
乙
乙
(填甲或乙),求出a=50
50
cm/s2.(3)在对本纸带的测量中,某同学只测量了如图2两组数据,若每两个相邻计数点间的时间间隔为T,测这个物体运动的加速度为a=
| S5-S2 |
| 3T2 |
| S5-S2 |
| 3T2 |
匀变速直线运动的物体,中间时刻的瞬时速度等于这段时间内的平均速度,某同学在“验证匀变速直线运动的小车速度随时间变化的规律”的实验中,如图给出了从0点开始,每5个点取一个计数点的纸带,其中0、1、2、3、4、5、6都为计数点.测得:s1=1.40cm,s2=1.90cm,s3=2.40cm,s4=2.88cm,s5=3.43cm,s6=3.90cm.(以下计算结果均保留三位有效数字)

(1)在计时器打出点1、2、3、4、5时,小车的速度分别为:v1=
(2)(4分)在对本纸带的测量中,某同学只测量了如下图两组数据,若每两个相邻计数点间的时间间隔为T,测这个物体运动的加速度为a=
(用S2、S5、T表示)

查看习题详情和答案>>

(1)在计时器打出点1、2、3、4、5时,小车的速度分别为:v1=
16.5
16.5
cm/s,v2=21.5
21.5
cm/s,v3=26.4
26.4
cm/s,v4=31.6
31.6
cm/s,v5=36.7
36.7
cm/s.(2)(4分)在对本纸带的测量中,某同学只测量了如下图两组数据,若每两个相邻计数点间的时间间隔为T,测这个物体运动的加速度为a=
| s5-s2 |
| 3T2 |
| s5-s2 |
| 3T2 |

 我们经常能在电视上看到这样的情景:站在悬崖下的人仰头望着生长在崖间的树,把手中的长绳抛向树干,由于绳端系着一块石头,所以绳便绕着树干缠了几圈,然后那人攀着长绳就上了崖顶.
我们经常能在电视上看到这样的情景:站在悬崖下的人仰头望着生长在崖间的树,把手中的长绳抛向树干,由于绳端系着一块石头,所以绳便绕着树干缠了几圈,然后那人攀着长绳就上了崖顶.(1)请你就此人攀着绳子向上而绳却不滑落下来提出一个和摩擦力有关的问题.
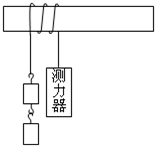
(2)小辉同学认为绳在不被拉断的前提下,能够承受的拉力F与绳子缠绕的圈数n会有某种关系,即如果绳子绕树3圈就可让一个质量为30kg的少年攀绳向上而不滑落,那么一个质量为60kg的人要通过此绳向上,绳子所绕圈数n就要大于3.于是他设计并做了实验.实验原理见图,图中每个钩码重为1.96N,在测力器一端施加向下的力,在使钩码静止时,从测力器上获得读数.下表是实验数据的记录.
| 圈数n | 0.5 | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | ||
| 钩码、 金属棒、 棉线 |
1个 钩码 |
测力计读数/N | 1.111 | 0.344 | 0.153 | 0.059 | 0.057 | 0.057 |
| 摩擦力/N | 0.849 | 1.616 | X | 1.901 | 1.903 | 1.903 | ||
| 2个 钩码 |
测力计读数/N | 2.242 | 0.682 | 0.312 | 0.061 | 0.043 | 0.043 | |
| 摩擦力/N | 1.678 | 3.238 | 3.608 | 3.859 | 3.877 | 3.877 | ||
| 钩码、 塑料棒、棉线 |
1个 钩码 |
测力计读数/N | 0.862 | 0.263 | 0.119 | 0.071 | 0.047 | 0.047 |
| 摩擦力/N | 1.098 | 1.697 | 1.841 | 1.889 | 1.913 | 1.913 | ||
| 2个 钩码 |
测力计读数/N | 1.736 | 0.535 | 0.228 | 0.071 | 0.047 | 0.047 | |
| 摩擦力/N | 2.184 | 3.385 | 3.692 | 3.849 | 3.873 | 3.873 | ||
(b)从以上的数据中你能得出的结论是
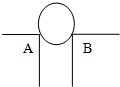 一个厚度均匀、质量分布均匀的金属空心球壳,质量为m,置于一支架A、B上,球壳半径与支架间距都是R,现缓慢从上端开口注水,将水注满时,水的质量也为m,则以下说法正确的是( )
一个厚度均匀、质量分布均匀的金属空心球壳,质量为m,置于一支架A、B上,球壳半径与支架间距都是R,现缓慢从上端开口注水,将水注满时,水的质量也为m,则以下说法正确的是( )