网址:http://m.1010jiajiao.com/timu_id_105197[举报]
一、二、选择题(共31分)
题号
1
2
3
4
5
6
7
8
9
答案
A
C
D
C
B
AC
AD
ACD
AD
三、填空题(共40分)
10.(1)21.0 400 (每空2分)
(2)① B C (每空2分) ② A (2分)
11.F/2 ? mg C (每空3分)
12.B(1)(4分)相反 早 (2)(4分) ACD (2)(4分) R/2
R/2
C(1)(4分)E  (2)(4分) BC (3)(4分)
(2)(4分) BC (3)(4分)
四、计算题(共49分)
13.解、(1)最后物块相对皮带静止,动能不变,摩擦力对物块做功为0
求得相对位移 ,
,
 (2)先以传送带为参考系考虑问题:开始时物块相对于传送带的速度大小为
(2)先以传送带为参考系考虑问题:开始时物块相对于传送带的速度大小为 v,方向与x轴成1350。滑动摩擦力方向总与相对运动方向相反,即与x轴成-450。如图所示。由于物块受到的外力为恒力,它相地于传送带做的是匀减速直线运动,至速度减为0,就不再受摩擦力作用,将与传送带保持相对静止。现在再转换到以地面为参考系:物块先做初速度为v(方向沿+y方向)、加速度为μg的匀变速曲线运动,加速度方向始终与皮带边缘成-45º夹角;然后物块随皮带一起沿+x方向做速度为v的匀速直线运动。
v,方向与x轴成1350。滑动摩擦力方向总与相对运动方向相反,即与x轴成-450。如图所示。由于物块受到的外力为恒力,它相地于传送带做的是匀减速直线运动,至速度减为0,就不再受摩擦力作用,将与传送带保持相对静止。现在再转换到以地面为参考系:物块先做初速度为v(方向沿+y方向)、加速度为μg的匀变速曲线运动,加速度方向始终与皮带边缘成-45º夹角;然后物块随皮带一起沿+x方向做速度为v的匀速直线运动。
物块在皮带上的运动(相对地面)x方向是初速为0的匀加速运动,vx=ax?t,y方向是初速为v的匀减速运动,vy=v-ay?t,其中ax=ay= .合速度为
.合速度为 ,即
,即 ,当
,当 时,
时, 有最小值,最小速度
有最小值,最小速度
(或者利用斜抛运动最高点速度最小求解)
(3)以地面为参考系,对整个运动过程应用动能定理,得摩擦力对物块做的功W=0。以传送带为参考系,整个运动过程物块动能的减小即等于生的热。得 。如果求生的热,应先求相对于传送带的位移。
。如果求生的热,应先求相对于传送带的位移。
 ,则生的热
,则生的热 。
。
14.(1)通过cd棒的电流方向 d→c,区域I内磁场方向为垂直于斜面向上
(2)对cd棒,F安=BIl=mgsinθ所以通过cd棒的电流大小I =
当ab棒在区域II内运动时cd棒消耗的电功率P=I2R=
(3)ab棒在到达区域II前做匀加速直线运动,a==gsinθ
cd棒始终静止不动,ab棒在到达区域II前、后,回路中产生的感应电动势不变,则ab棒在区域II中一定做匀速直线运动
可得;=Blvt =Blgsinθt x 所以t x=
ab棒在区域II中做匀速直线运动的速度vt=
则ab棒开始下滑的位置离EF的距离h= a tx2+
(4) ab棒在区域II中运动的时间t2==
ab棒从开始下滑至EF的总时间t= tx+t2=2 ε=Blvt =Bl
ab棒从开始下滑至EF的过程中闭合回路中产生的热量:Q=εIt=4mglsinθ
15.(1) 粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,即
粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,即
 ,则
,则
(2)设cd中心为O,向c端偏转的 粒子,当圆周轨迹与cd相切时偏离O最远,
粒子,当圆周轨迹与cd相切时偏离O最远,
设切点为P,对应圆心O1,如图所示,则由几何关系得:
向d端偏转的 粒子,当沿Sb方向射入时,偏离O最远,设此时圆周轨迹与cd交于Q点,对应圆心O2,如图所示,则由几何关系得:
粒子,当沿Sb方向射入时,偏离O最远,设此时圆周轨迹与cd交于Q点,对应圆心O2,如图所示,则由几何关系得:
故金箔cd被 粒子射中区域的长度L=
粒子射中区域的长度L= 
(3)设从Q点穿出的 粒子的速度为
粒子的速度为 ,因半径O2Q∥场强E,则
,因半径O2Q∥场强E,则 ⊥E,故穿出的
⊥E,故穿出的 粒子在电场中做类平抛运动,
粒子在电场中做类平抛运动,
沿速度 方向做匀速直线运动,位移
方向做匀速直线运动,位移
沿场强E方向做匀加速直线运动,位移
 ,
,
 如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10-27kg,电荷量q=3.2×10-19C,初速度v=3.2×106m/s.(sin37°=0.6,cos37°=0.8)求:
如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10-27kg,电荷量q=3.2×10-19C,初速度v=3.2×106m/s.(sin37°=0.6,cos37°=0.8)求:(1)α粒子在磁场中作圆周运动的轨道半径R;
(2)金箔cd被α粒子射中区域的长度L;
(3)设打在金箔上d端离cd中心最远的α粒子穿出金箔进入电场,若穿出金箔时速度方向与射入金箔时速度方向相同,在电场中运动通过N点,SN⊥ab且SN=40cm,则此α粒子从金箔上穿出时,损失的动能△EK为多少?
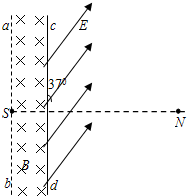 如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10-27kg,电荷量q=+3.2×10-19C,初速度
如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10-27kg,电荷量q=+3.2×10-19C,初速度v=3.2×106m/s.不计粒子重力(sin37°=0.6,cos37°=0.8)
求:(1)α粒子在磁场中作圆周运动的轨道半径R;
(2)金箔cd被α粒子射中区域的长度L;
(3)设打在金箔上d端离cd中心最远的α粒子,速度方向不变穿出金箔进入电场.在电场中运动通过N点,SN⊥ab且SN=40cm,则此α粒子从金箔上穿出时的速度大小为多少?
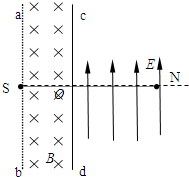 如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105 N/C,方向与金箔平行竖直向上.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率不相同的α粒子,但初速率大小在1.0×106m/s<V≤3.2×106m/s 之间.已知:mα=6.64×10-27Kg,qα=3.2×10-19C,SN⊥ab且SN=18cm.试求:
如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105 N/C,方向与金箔平行竖直向上.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率不相同的α粒子,但初速率大小在1.0×106m/s<V≤3.2×106m/s 之间.已知:mα=6.64×10-27Kg,qα=3.2×10-19C,SN⊥ab且SN=18cm.试求:(1)金箔cd上半部Oc上被α粒子射中最大区域的长度L;
(2)若有沿Sb方向射出的α粒子经磁场作用恰好垂直打在金箔cd上并沿入射方向穿出金箔进入电场,在电场中运动通过N点,则此α粒子从金箔上穿出时,损失的动能△EK为多少?
如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10-27kg,电荷量q = 3.2×10-19C,初速度v = 3.2×106m/s。(sin37°= 0.6,cos37°= 0.8)求:
(1)α粒子在磁场中作圆周运动的轨道半径R;
(2)金箔cd被α粒子射中区域的长度L;
(3)设打在金箔上d端离cd中心最远的α粒子穿出金箔进入电场,在电场中运动通过N点,SN⊥ab且SN = 40cm,则此α粒子从金箔上穿出时,损失的动能△EK为多少?
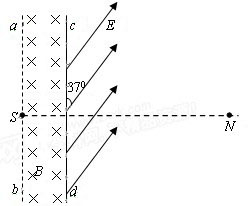
如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量
m=6.64×10-27kg,电荷量q =+3.2×10-19C,初速度
v = 3.2×106m/s。不计粒子重力(sin37°= 0.6,
cos37°= 0.8)求:
(1)α粒子在磁场中作圆周运动的轨道半径R;
(2)金箔cd被α粒子射中区域的长度L;
(3)设打在金箔上d端离cd中心最远的α粒子,速度方向不变穿出金箔进入电场。在电场中运动通过N点,SN⊥ab且SN = 40cm,则此α粒子从金箔上穿出时的速度大小为多少?
查看习题详情和答案>>