网址:http://m.1010jiajiao.com/timu_id_10509[举报]
一.选择题:(本大题共15个题;每小题3分,共45分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
答案
B
C
A
C
D
A
B
A
D
B
A
B
D
A
A
 二.填空题:(本大题共5小题;每小题3分,共15分。)
二.填空题:(本大题共5小题;每小题3分,共15分。)
16.4 17. 36 ; 18. 20000; 19.
20.109
三.解答题:(本大题共6小题,共40分。解答应写出文字说明、证明过程或演算步骤。)
21.
解:(1)原式 ---1分
---1分
 ---2分
---2分
 ---3分
---3分
(2)
解:去分母得2x-5=3(2x-1)
即2x-5=6x-3---1分
∴4x=-2
x= ---2分
---2分
当x= 时,2x-1≠0
时,2x-1≠0
所以x= 是原方程的解---3分
是原方程的解---3分
22.(本题6分)
(1) C ---2分
(2)没有考虑 ---4分
---4分
(3) ---6分
---6分
23.(本题7分)
解(1)当x 30时,设函数关系式为y=kx+b
30时,设函数关系式为y=kx+b
则 -------2分
-------2分
解得
所以y=3x-30-------4分
(2)4月份上网20小时,应付上网费60元-------5分
(3) 由75=3x-30解得x=35,所以5月份上网35个小时. -------7分
24.(本题7分)
解:⑴设蓝球个数为 个
-------1分
个
-------1分
则由题意得 -------2分
-------2分

 答:蓝球有1个
--------3分
答:蓝球有1个
--------3分
--------4分
---------5分
∴ 两次摸到都是白球的概率 =
= ----------7分
----------7分
 25.(本题6分)
25.(本题6分)
证明:(1)∵AE=CF
∴AE+EF=CF+FE即AF=CE --------- 1分
又ABCD是平行四边形,∴AD=CB,AD∥BC
∴∠DAF=∠BCE ---------2分
在△ADF与△CBE中
 ---------3分
---------3分
∴△ADF≌△CBE(SAS)---------4分
(2)∵△ADF≌△CBE
∴∠DFA=∠BEC ---------5分
∴DF∥EB---------6分
26.(本题8分)
(1)由已知可得∠A,OE=60o , A,E=AE
由A′E// 轴,得△OA,E是直角三角形,
轴,得△OA,E是直角三角形,
设A,的坐标为(0,b)
AE=A,E= ,OE=2b
,OE=2b

所以b=1,A,、E的坐标分别是(0,1)与( ,1) --------3分
,1) --------3分
(2) 因为A,、E在抛物线上,所以

所以 ,函数关系式为
,函数关系式为
由 得
得
与x轴的两个交点坐标分别是( ,0)与(
,0)与( ,0)--------6分
,0)--------6分
(3) 不可能使△A′EF成为直角三角形。
∵∠FA,E=∠FAE=60o,若△A′EF成为直角三角形,只能是∠A,EF=90o或∠A,FE=90o
若∠A,EF=90o,利用对称性,则∠AEF=90o, A,、E、A三点共线,O与A重合,与已知矛盾;
同理若∠A,FE=90o也不可能
所以不能使△A′EF成为直角三角形。--------8分
(本题满分12分)
已知直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.

1.(1)填空:菱形ABCD的边长是 ▲ 、面积是 ▲ 、 高BE的长是 ▲ ;
2.(2)探究下列问题:
若点P的速度为每秒1个单位,点Q的速度为每秒2个单位.当点Q在线段BA上时
② △APQ的面积S关于t的函数关系式,以及S的最大值;
3.(3)在运动过程中是否存在某一时刻使得△APQ为等腰三角形,若存在求出t的值;若不存在说明理由.
查看习题详情和答案>>
(本题满分10分)
已知:如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF∶GF=1∶2,求矩形DEFG的周长.
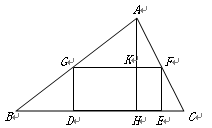
查看习题详情和答案>>
(本题满分7分)如图,已知一次函数y=kx+b的图象与反比例函数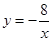
的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
求:(1)一次函数的解析式;
(2)△ABC的面积.
查看习题详情和答案>>
(本题满分12分)已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF= 90°,∠DEF = 45°,AC =6cm,BC = 6 cm,EF = 12cm.
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s).解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)当t为何值时,△PQE是直角三角形?
(3)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
(4)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由
查看习题详情和答案>>