摘要：③若a≥4时.得f (x)在上的最小值.此时>0恒成立.

网址：http://m.1010jiajiao.com/timu_id_102386[举报]

已知函数f(x)=

在区间[m，n]上为增函数，且f（m）f（n）=-4．
（1）当a=3时，求m，n的值；
（2）当f（n）-f（m）最小时，
①求a的值；
②若P（x₁，y₁），Q（x₂，y₂）（a＜x₁＜x₂＜n）是f（x）图象上的两点，且存在实数x₀使得f′(x0)=

，证明：x₁＜x₀＜x₂．查看习题详情和答案>>

已知函数f(x)=

的单调递增区间为[m，n]
（1）求证f（m）f（n）=-4；
（2）当n-m取最小值时，点p（x₁，y₁），Q（x₂，y₂）（a＜x₁＜x₂＜n），是函数f（x）图象上的两点，若存在x₀使得f′（x₀）=

，x求证x₁＜|x₀|＜x₂．

查看习题详情和答案>>

已知a＞0，函数 $数学公式$ （其中e为自然对数的底数）．
（Ⅰ）求函数f（x）在区间（0，e]上的最小值；
（Ⅱ）设g（x）=x²-2bx+4，当a=1时，若对任意x₁∈（0，e），存在x₂∈[1，3]，使得f（x₁）≥g（x₂），求实数b的取值范围．

查看习题详情和答案>>

已知a＞0，函数f(x)=

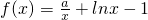+lnx-1（其中e为自然对数的底数）．
（Ⅰ）求函数f（x）在区间（0，e]上的最小值；
（Ⅱ）设g（x）=x²-2bx+4，当a=1时，若对任意x₁∈（0，e），存在x₂∈[1，3]，使得f（x₁）≥g（x₂），求实数b的取值范围．

查看习题详情和答案>>

已知a＞0，函数

（其中e为自然对数的底数）．
（Ⅰ）求函数f（x）在区间（0，e]上的最小值；
（Ⅱ）设g（x）=x²-2bx+4，当a=1时，若对任意x₁∈（0，e），存在x₂∈[1，3]，使得f（x₁）≥g（x₂），求实数b的取值范围．
查看习题详情和答案>>