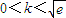题目内容
已知a>0,函数 (其中e为自然对数的底数).
(其中e为自然对数的底数).(Ⅰ)求函数f(x)在区间(0,e]上的最小值;
(Ⅱ)设g(x)=x2-2bx+4,当a=1时,若对任意x1∈(0,e),存在x2∈[1,3],使得f(x1)≥g(x2),求实数b的取值范围.
【答案】分析:(Ⅰ)令 ,可得x=a,进而a≥e时,函数f(x)在区间(0,e]是减函数;0<a<e时,函数f(x)在区间(0,a]是减函数,[a,e]是增函数,故可求函数f(x)在区间(0,e]上的最小值;
,可得x=a,进而a≥e时,函数f(x)在区间(0,e]是减函数;0<a<e时,函数f(x)在区间(0,a]是减函数,[a,e]是增函数,故可求函数f(x)在区间(0,e]上的最小值;
(Ⅱ)由(Ⅰ)可知,a=1时,函数f(x)在x1∈(0,e)的最小值为0,对任意x1∈(0,e),存在x2∈[1,3],使得f(x1)≥g(x2),则需要f(x)min≥g(x)min,根据g(x)=(x-b)2+4-b2,即可求出满足条件的实数b的取值范围.
解答:解:(Ⅰ)令 ,可得x=a
,可得x=a
若a≥e时,函数f(x)在区间(0,e]是减函数,∴ ;
;
0<a<e时,函数f(x)在区间(0,a]是减函数,[a,e]是增函数,∴f(x)min=f(a)=lna;
(Ⅱ)由(Ⅰ)可知,a=1时,函数f(x)在x1∈(0,e)的最小值为0,
对任意x1∈(0,e),存在x2∈[1,3],使得f(x1)≥g(x2),则需要f(x)min≥g(x)min,
g(x)=(x-b)2+4-b2
当b≤1时,g(x)min=g(1)=5-2b≤0不成立
当b≥3时,g(x)min=g(3)=13-6b≤0恒成立
当1<b<3时,g(x)min=g(b)=4-b2≤0此时2≤b<3
综上知,满足条件的实数b的取值范围{b|b≥2}
点评:本题考查导数知识的运用,考查函数的单调性与最值,解题的关键是将对任意x1∈(0,e),存在x2∈[1,3],使得f(x1)≥g(x2),转化为f(x)min≥g(x)min求解.
 ,可得x=a,进而a≥e时,函数f(x)在区间(0,e]是减函数;0<a<e时,函数f(x)在区间(0,a]是减函数,[a,e]是增函数,故可求函数f(x)在区间(0,e]上的最小值;
,可得x=a,进而a≥e时,函数f(x)在区间(0,e]是减函数;0<a<e时,函数f(x)在区间(0,a]是减函数,[a,e]是增函数,故可求函数f(x)在区间(0,e]上的最小值;(Ⅱ)由(Ⅰ)可知,a=1时,函数f(x)在x1∈(0,e)的最小值为0,对任意x1∈(0,e),存在x2∈[1,3],使得f(x1)≥g(x2),则需要f(x)min≥g(x)min,根据g(x)=(x-b)2+4-b2,即可求出满足条件的实数b的取值范围.
解答:解:(Ⅰ)令
 ,可得x=a
,可得x=a若a≥e时,函数f(x)在区间(0,e]是减函数,∴
 ;
;0<a<e时,函数f(x)在区间(0,a]是减函数,[a,e]是增函数,∴f(x)min=f(a)=lna;
(Ⅱ)由(Ⅰ)可知,a=1时,函数f(x)在x1∈(0,e)的最小值为0,
对任意x1∈(0,e),存在x2∈[1,3],使得f(x1)≥g(x2),则需要f(x)min≥g(x)min,
g(x)=(x-b)2+4-b2
当b≤1时,g(x)min=g(1)=5-2b≤0不成立
当b≥3时,g(x)min=g(3)=13-6b≤0恒成立
当1<b<3时,g(x)min=g(b)=4-b2≤0此时2≤b<3
综上知,满足条件的实数b的取值范围{b|b≥2}
点评:本题考查导数知识的运用,考查函数的单调性与最值,解题的关键是将对任意x1∈(0,e),存在x2∈[1,3],使得f(x1)≥g(x2),转化为f(x)min≥g(x)min求解.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
已知k>0,函数f(x)=kx2-lnx在其定义域上有两个零点,则实数k的取值范围是( )
A、k>
| ||||
B、0<k<
| ||||
C、k>
| ||||
D、0<k<
|