网址:http://m.1010jiajiao.com/timu_id_102326[举报]
已知数列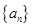 的前
的前 项和为
项和为 ,且
,且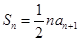 (
(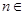 N*),其中
N*),其中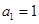 .
.
(Ⅰ) 求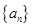 的通项公式;
的通项公式;
(Ⅱ) 设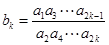 (
(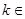 N*).
N*).
①证明: 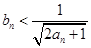 ;
;
② 求证: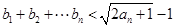 .
.
【解析】本试题主要考查了数列的通项公式的求解和运用。运用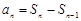 关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到
关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到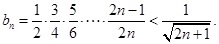 ,②由于
,②由于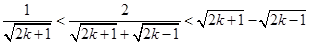 ,
,
所以 利用放缩法,从此得到结论。
利用放缩法,从此得到结论。
解:(Ⅰ)当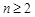 时,由
时,由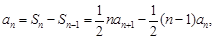 得
得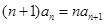 . ……2分
. ……2分
若存在 由
由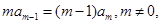 得
得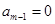 ,
,
从而有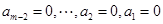 ,与
,与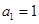 矛盾,所以
矛盾,所以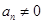 .
.
从而由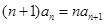 得
得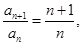 得
得 . ……6分
. ……6分
(Ⅱ)①证明: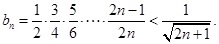
证法一:∵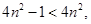 ∴
∴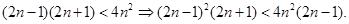
∴
∴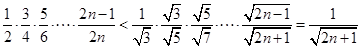 .…………10分
.…………10分
证法二: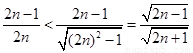 ,下同证法一.
……10分
,下同证法一.
……10分
证法三:(利用对偶式)设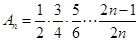 ,
,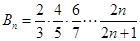 ,
,
则 .又
.又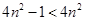 ,也即
,也即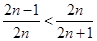 ,所以
,所以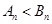 ,也即
,也即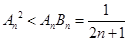 ,又因为
,又因为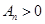 ,所以
,所以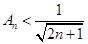 .即
.即
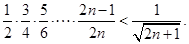 ………10分
………10分
证法四:(数学归纳法)①当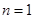 时,
时, 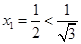 ,命题成立;
,命题成立;
②假设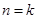 时,命题成立,即
时,命题成立,即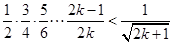 ,
,
则当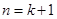 时,
时,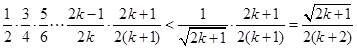
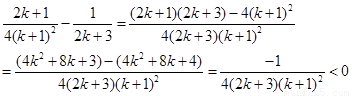
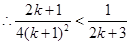 即
即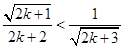
即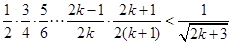
故当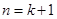 时,命题成立.
时,命题成立.
综上可知,对一切非零自然数 ,不等式②成立. ………………10分
,不等式②成立. ………………10分
②由于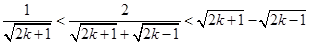 ,
,
所以 ,
,
从而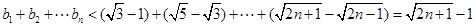 .
.
也即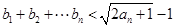
查看习题详情和答案>>
设f (x)=sin 2x+ (sin x-cos x)(sin x+cos x),其中x∈R.
(sin x-cos x)(sin x+cos x),其中x∈R.
(Ⅰ) 该函数的图象可由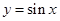
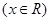 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
(Ⅱ)若f (θ)= ,其中
,其中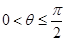 ,求cos(θ+
,求cos(θ+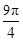 )的值;
)的值;
【解析】第一问中,
即 变换分为三步,①把函数
变换分为三步,①把函数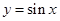 的图象向右平移
的图象向右平移 ,得到函数
,得到函数 的图象;
的图象;
②令所得的图象上各点的纵坐标不变,把横坐标缩短到原来的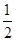 倍,得到函数
倍,得到函数 的图象;
的图象;
③令所得的图象上各点的横坐标不变,把纵坐标伸长到原来的2倍,得到函数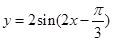 的图象;
的图象;
第二问中因为 ,所以
,所以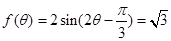 ,则
,则 ,又
,又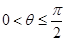
 ,
,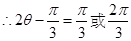 ,从而
,从而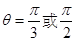
进而得到结论。
(Ⅰ) 解: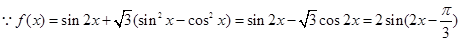
即 。…………………………………3分
。…………………………………3分
变换的步骤是:
①把函数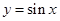 的图象向右平移
的图象向右平移 ,得到函数
,得到函数 的图象;
的图象;
②令所得的图象上各点的纵坐标不变,把横坐标缩短到原来的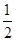 倍,得到函数
倍,得到函数 的图象;
的图象;
③令所得的图象上各点的横坐标不变,把纵坐标伸长到原来的2倍,得到函数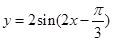 的图象;…………………………………3分
的图象;…………………………………3分
(Ⅱ) 解:因为 ,所以
,所以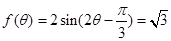 ,则
,则 ,又
,又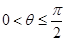
 ,
,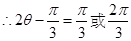 ,从而
,从而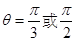 ……2分
……2分
(1)当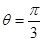 时,
时, ;…………2分
;…………2分
(2)当 时;
时;
查看习题详情和答案>>
若函数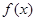 在定义域内存在区间
在定义域内存在区间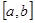 ,满足
,满足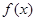 在
在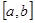 上的值域为
上的值域为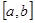 ,则称这样的函数
,则称这样的函数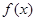 为“优美函数”.
为“优美函数”.
(Ⅰ)判断函数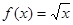 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出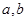 ;若不是,说明理由;
;若不是,说明理由;
(Ⅱ)若函数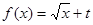 为“优美函数”,求实数
为“优美函数”,求实数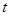 的取值范围.
的取值范围.
【解析】第一问中,利用定义,判定由题意得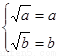 ,由
,由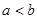 ,所以
,所以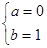
第二问中, 由题意得方程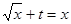 有两实根
有两实根
设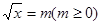 所以关于m的方程
所以关于m的方程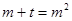 在
在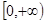 有两实根,
有两实根,
即函数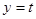 与函数
与函数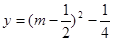 的图像在
的图像在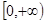 上有两个不同交点,从而得到t的范围。
上有两个不同交点,从而得到t的范围。
解(I)由题意得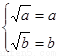 ,由
,由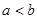 ,所以
,所以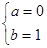 (6分)
(6分)
(II)由题意得方程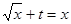 有两实根
有两实根
设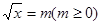 所以关于m的方程
所以关于m的方程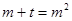 在
在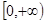 有两实根,
有两实根,
即函数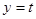 与函数
与函数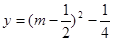 的图像在
的图像在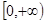 上有两个不同交点。
上有两个不同交点。
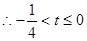
查看习题详情和答案>>
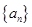 的各项均为正数.若对任意的
的各项均为正数.若对任意的 ,存在
,存在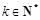 ,使得
,使得 成立,则称数列
成立,则称数列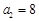 ,
,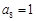 ,求
,求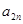 ;
;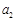 ,
,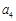 ,
,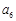 ,
, ,…成等比数列,且公比
,…成等比数列,且公比 ,
,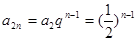
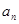 }是“j4型”数列,得
}是“j4型”数列,得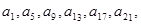 ,…成等比数列,设公比为t. 由{
,…成等比数列,设公比为t. 由{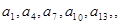 ,…成等比数列,设公比为
,…成等比数列,设公比为 ;
;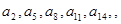 ,…成等比数列,设公比为
,…成等比数列,设公比为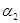 ;
; …成等比数列,设公比为
…成等比数列,设公比为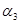 ;
;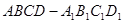 中,
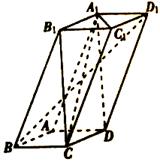
中,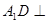 平面
平面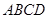 ,底面
,底面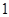 的正方形,侧棱
的正方形,侧棱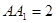 .
.
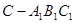 的体积;
的体积;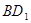 与平面
与平面 所成角的正弦值;
所成角的正弦值;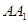 上存在一点
上存在一点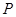 ,使得
,使得 ,当二面角
,当二面角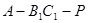 的大小为
的大小为 时,求实数
时,求实数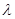 的值.
的值.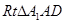 中,
中,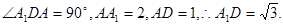
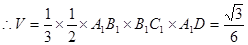 .
(3’)
.
(3’) ,则
,则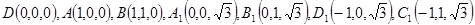 (4’)
(4’)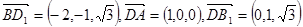 ,设平面
,设平面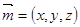 ,
, 得
得 ,
(5’)
,
(5’) ,
, 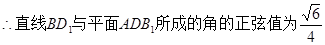 . (7’)
. (7’)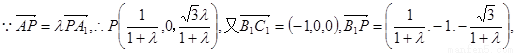
 的法向量为
的法向量为 ,由
,由 得
得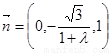 ,
(10’)
,
(10’)