0 53913 53921 53927 53931 53937 53939 53943 53949 53951 53957 53963 53967 53969 53973 53979 53981 53987 53991 53993 53997 53999 54003 54005 54007 54008 54009 54011 54012 54013 54015 54017 54021 54023 54027 54029 54033 54039 54041 54047 54051 54053 54057 54063 54069 54071 54077 54081 54083 54089 54093 54099 54107 447348
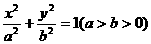 的左焦点为
的左焦点为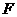 ,上顶点为
,上顶点为 ,过点
,过点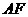 垂直的直线分别交椭圆和
垂直的直线分别交椭圆和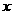 轴正半轴于
轴正半轴于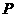 ,
,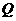 两点,且
两点,且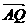 所成的比为8∶5.
所成的比为8∶5.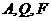 三点的圆恰好与直线
三点的圆恰好与直线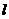 :
: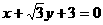 相切,求椭圆方程.
相切,求椭圆方程.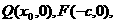 其中
其中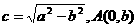 .
.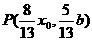 , 2分
, 2分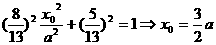 .①, 4分
.①, 4分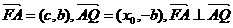 ,
,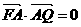 .
.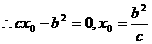 .②, 5分
.②, 5分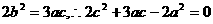 .
.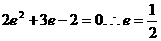 . 6分
. 6分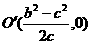 ,
,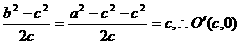 , 8分
, 8分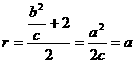 . 10分
. 10分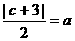 ,
,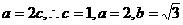 .
. . 12分
. 12分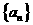 的前n项和为
的前n项和为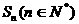 ,且
,且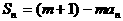 对任意自然数都成立,其中m为常数,且
对任意自然数都成立,其中m为常数,且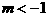 。
。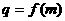 ,数列
,数列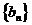 满足:
满足: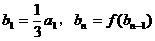
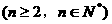 ,试问当m为何值时,
,试问当m为何值时,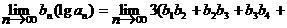
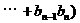 成立?
成立?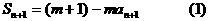
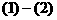 得:
得: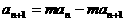 ,即
,即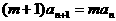 对任意
对任意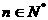 都成立
都成立
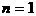 时,
时,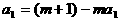
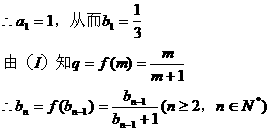
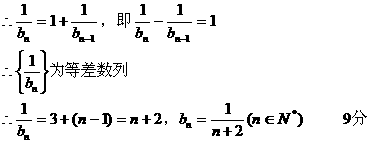
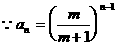
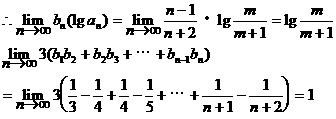
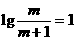
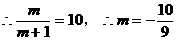 13分
13分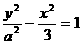 的两个焦点分别为
的两个焦点分别为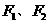 ,离心率为2。
,离心率为2。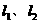 的方程;
的方程;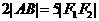 ,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线;
,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线;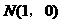 能否作出直线
能否作出直线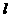 ,使
,使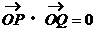 。若存在,求出直线
。若存在,求出直线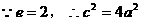
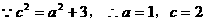
 ,渐近线方程为
,渐近线方程为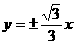 4分
4分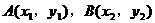 ,AB的中点
,AB的中点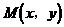
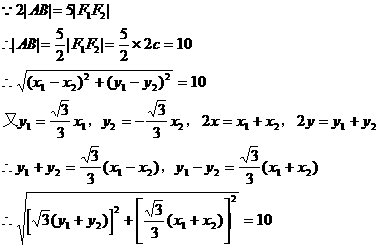
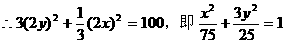
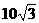 ,短轴长为
,短轴长为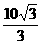 的椭圆。(9分)
的椭圆。(9分)
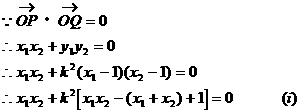
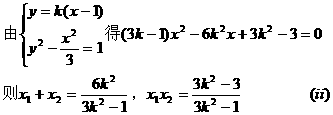
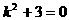
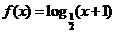 ,当点
,当点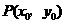 在
在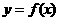 的图像上移动时,
的图像上移动时,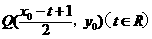 在函数
在函数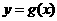 的图像上移动.
的图像上移动.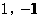 ),点Q也在
),点Q也在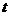 的值;
的值;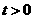 时,试探求一个函数
时,试探求一个函数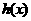 使得
使得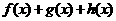 在限定定义域为
在限定定义域为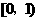 时有最小值而没有最大值.
时有最小值而没有最大值.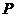 坐标为(
坐标为(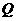 的坐标为
的坐标为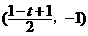 ,…………2分
∵点
,…………2分
∵点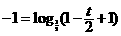 ,即
,即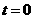 .……5分
.……5分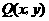 在
在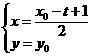 ,即
,即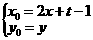 ……………………………………8分
而
……………………………………8分
而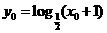 代入得,
代入得,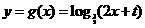 为所求.…………………………………11分
为所求.…………………………………11分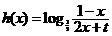 ;或
;或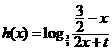 等. …………………15分
如:当
等. …………………15分
如:当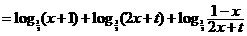
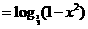
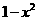 在
在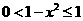 故
故 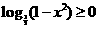 ,
即
,
即 ,但没有最大值.………………………18分
,但没有最大值.………………………18分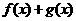 的和运算);②由于
的和运算);②由于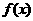 和
和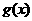 都是以
都是以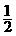 为底的对数,所以构造的函数
为底的对数,所以构造的函数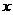 的二次函数,该二次函数的图像的对称轴应在直线
的二次函数,该二次函数的图像的对称轴应在直线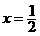 的左侧(否则真数会有最小值,对数就有最大值了),考虑到该二次函数的图像与
的左侧(否则真数会有最小值,对数就有最大值了),考虑到该二次函数的图像与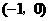 ,故对称轴又应该是
,故对称轴又应该是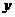 轴或在
轴或在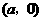 ,则
,则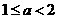 ,且抛物线开口向下.
,且抛物线开口向下.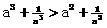 成立。
成立。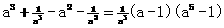 ,∵a>1,∴
,∵a>1,∴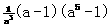 >0,
>0,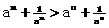 (12¢)
(12¢)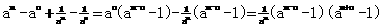 (14¢)
(14¢)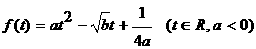 的最大值为正实数,集合
的最大值为正实数,集合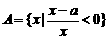 ,集合
,集合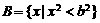 。
。 和
和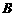 ;
;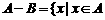 且
且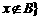 。
。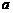 ,
,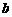 ,
,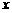 均为整数,且
均为整数,且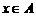 。
。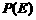 为
为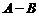 的概率,
的概率,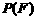 为
为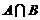 的概率,写出
的概率,写出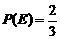 ,
,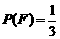 。
。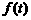 中,
中,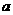 ,
,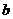 是(2)中
是(2)中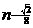 ,n]上的最大值函数
,n]上的最大值函数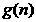 的表达式。
的表达式。 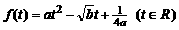 ,配方得
,配方得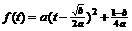 ,由
,由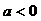 得最大值
得最大值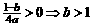 。……………………………………………………………3分
。……………………………………………………………3分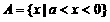 ,
,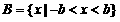 。…………………………6分
。…………………………6分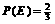 ,
,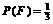 。可以使①
。可以使①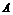 中有3个元素,
中有3个元素,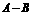 中有2个元素,
中有2个元素, 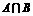 中有1个元素。则
中有1个元素。则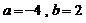 。…………………………………………………9分
。…………………………………………………9分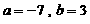 …………………………………………………………………………12分
…………………………………………………………………………12分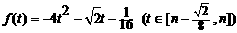 …………………………13分
…………………………13分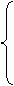
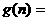
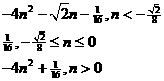 ………………………………………………18分
………………………………………………18分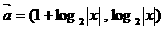 ,
,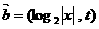
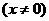 .
.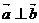 ,求实数x的值;
,求实数x的值;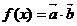 具备的性质.
具备的性质.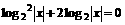 ……2分
……2分 ……4分
……4分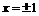 ,或
,或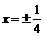 ……6分
……6分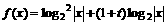 ……8分
……8分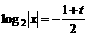 即
即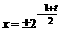 时,
时,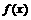 取得最小值
取得最小值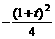 (写出值域为
(写出值域为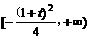 也可);
也可);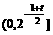 上递减,
上递减,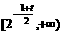 上递增;由对称性,在
上递增;由对称性,在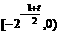 上递增,在
上递增,在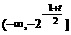 递减
……14分
递减
……14分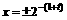 )等皆可。写出函数的定义域不得分,写错扣1分
)等皆可。写出函数的定义域不得分,写错扣1分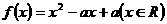 同时满足:①不等式
同时满足:①不等式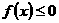 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在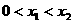 ,使得不等式
,使得不等式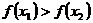 成立。
成立。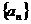 的前
的前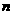 项和
项和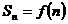 ,
,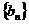 ,(写出
,(写出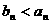 ,且
,且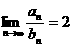 ,并说明理由;
,并说明理由;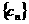 中,所有满足
中,所有满足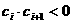 的正整数
的正整数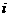 的个数称为这个数列
的个数称为这个数列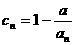 (
(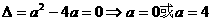 ,
,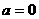 时,函数
时,函数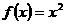 在
在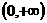 上递增,故不存在
上递增,故不存在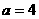 时,函数
时,函数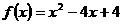 在
在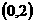 上递减,故存在
上递减,故存在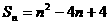 ,
,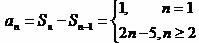
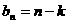 ,∵对任意的正整数
,∵对任意的正整数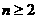 时,
时,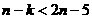 恒成立,即
恒成立,即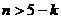 恒成立,即
恒成立,即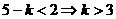 ,
,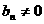 ,∴
,∴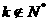 ,∴
,∴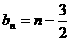 ,等等。
,等等。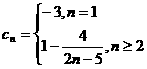 ,
,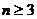 时,
时,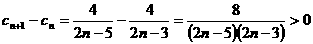 ,
,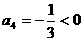 ,由
,由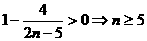 ,
,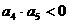 ,即
,即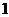 个变号数;
个变号数;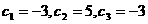 ,即
,即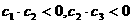 ,
,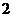 个。
个。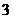 个变号数,即变号数为
个变号数,即变号数为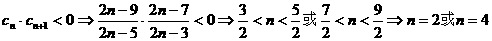 ;
;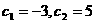 ,∴
,∴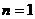 时也有
时也有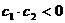 。
。