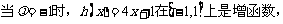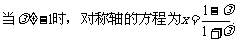0 53756 53764 53770 53774 53780 53782 53786 53792 53794 53800 53806 53810 53812 53816 53822 53824 53830 53834 53836 53840 53842 53846 53848 53850 53851 53852 53854 53855 53856 53858 53860 53864 53866 53870 53872 53876 53882 53884 53890 53894 53896 53900 53906 53912 53914 53920 53924 53926 53932 53936 53942 53950 447348
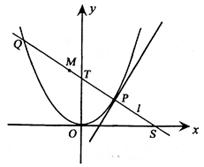 如图,P是抛物线C:y=
如图,P是抛物线C:y=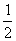 x2上一点,直线l过点P且与抛物线C交于另一点Q.
x2上一点,直线l过点P且与抛物线C交于另一点Q.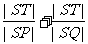 的取值范围.
的取值范围.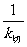 =-
=-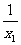 ,
,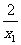 x-x12-2=0.
x-x12-2=0.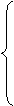 x0=
x0=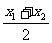 =-
=-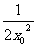 +1(x0≠0),
+1(x0≠0),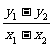 =kl=-
=kl=-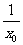 ,
,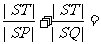
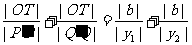 .
. y=
y=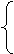 y1+y2=2(k2+b),
y1+y2=2(k2+b),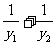 )≥2|b|
)≥2|b|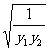 =2|b|
=2|b|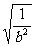 =2.
=2. ).
).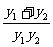 =|b|
=|b|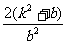 .
.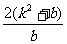 =
=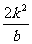 +2>2;
+2>2;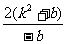 .
.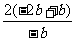 =2.
=2.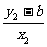 =
=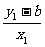 .
.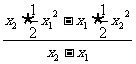 =-
=-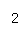
 ∴
∴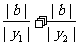 =
=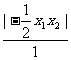 +
+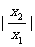 +
+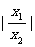 ≥2.
≥2.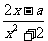 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.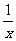 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.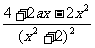 =
=
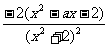 ,
,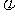 (x)=x2-ax-2,
(x)=x2-ax-2,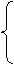
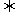
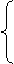
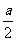 ≥0,
≥0,
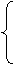 x1+x2=a,
x1+x2=a,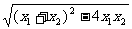 =
=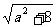 .
.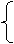
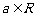 ,函数
,函数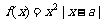 .
.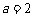 时,求使
时,求使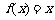 成立的
成立的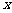 的集合;
的集合;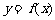 在区间
在区间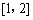 上的最小值.
上的最小值.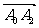 的坐标;
的坐标;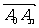 的坐标.
的坐标.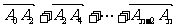 ,
,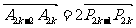 ,得
,得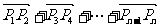 )=2({1,2}+{1,23}+┄+{1,2n-1})=2{
)=2({1,2}+{1,23}+┄+{1,2n-1})=2{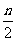 ,
,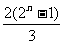 }={n,
}={n,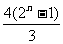 }
}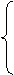 f(x)·g(x) 当x∈Df且x∈Dg
f(x)·g(x) 当x∈Df且x∈Dg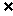 Dg
Dg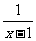 ,g(x)=x2,x∈R,写出函数h(x)的解析式;
,g(x)=x2,x∈R,写出函数h(x)的解析式;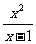 x∈(-∞,1)∪(1,+∞)
x∈(-∞,1)∪(1,+∞)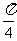
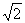 sin2x, α=
sin2x, α=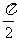 ,g(x)=f(x+α)= 1+
,g(x)=f(x+α)= 1+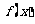 和
和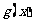 的图象关于原点对称,且
的图象关于原点对称,且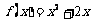 .
.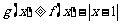 ;
;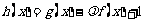 在
在 上是增函数,求实数
上是增函数,求实数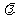 的取值范围.
的取值范围.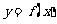 的图象上任意一点
的图象上任意一点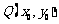 关于原点的对称点为
关于原点的对称点为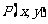 ,则
,则
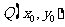 在函数
在函数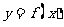 的图象上
的图象上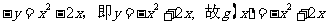
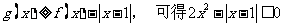
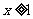 时,
时,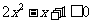 ,此时不等式无解.
,此时不等式无解.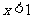 时,
时,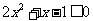 ,解得
,解得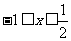 .
.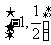 .
.