0 53621 53629 53635 53639 53645 53647 53651 53657 53659 53665 53671 53675 53677 53681 53687 53689 53695 53699 53701 53705 53707 53711 53713 53715 53716 53717 53719 53720 53721 53723 53725 53729 53731 53735 53737 53741 53747 53749 53755 53759 53761 53765 53771 53777 53779 53785 53789 53791 53797 53801 53807 53815 447348
 ,对于中点公式要熟记
,对于中点公式要熟记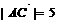 ,
,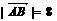 ,
,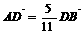 ,
,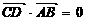 。
。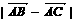 ;
;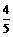 ,
,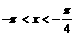 ,求sinx
,求sinx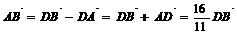
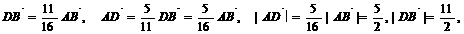
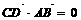 ∴CD⊥AB,在Rt△BCD中BC2=BD2+CD2,
∴CD⊥AB,在Rt△BCD中BC2=BD2+CD2, 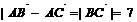 ……6分
……6分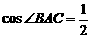 ∴
∴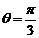 ……8分
……8分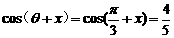
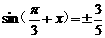
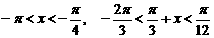 如果
如果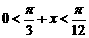 ,
,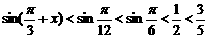 ∴
∴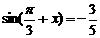 ……10分
……10分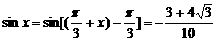
 ,
,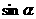 ),b=(
),b=(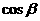 ,
,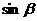 ),a与b之间有关系式|ka+b|=
),a与b之间有关系式|ka+b|=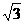 |a-kb|,其中k>0.
|a-kb|,其中k>0.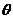 的大小.
的大小.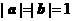 .
.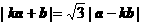 ,∴
,∴ 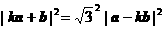 .∴
.∴ 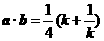 .
.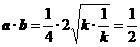 .
.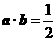 ∴
∴ 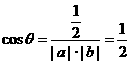 . ∴
. ∴ 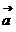 =(
=(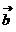 = (
= (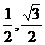 ).
).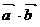 ;
;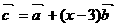 ,
,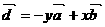 (其中
(其中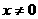 ),若
),若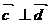 ,试求函数关系式
,试求函数关系式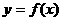 并解不等式
并解不等式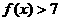 .(1)
.(1)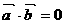 ;
; 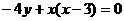 ,
, 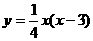 ;
; 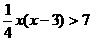 变形得:
变形得: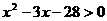 ,解得
,解得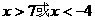 .
.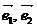 是平面内不共线两向量,已知
是平面内不共线两向量,已知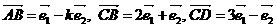 ,若
,若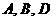 三点共线,则
三点共线,则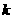 的值是
的值是 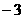 C.
C.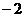 D.
D.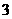
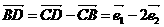 ,又A、B、D三点共线,则
,又A、B、D三点共线,则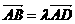 .即
.即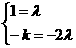 ,∴
,∴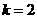 ,故选
,故选 .
.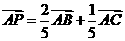 ,
, 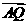 =
=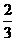
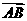 +
+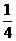
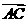 ,则△ABP的面积与△ABQ的面积之比为
,则△ABP的面积与△ABQ的面积之比为 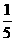 B.
B. 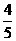 C.
C.
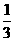
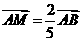 ,
,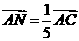 ,则
,则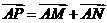 .
.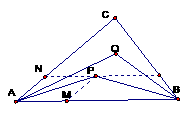 由平行四边形法则,知NP∥AB,所以
由平行四边形法则,知NP∥AB,所以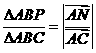 =
=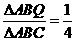 .故
.故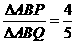 ,选B.
,选B.
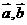 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么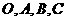 为空间四点,且向量
为空间四点,且向量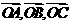 不构成空间的一个基底,那么点
不构成空间的一个基底,那么点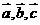 是空间的一个基底,则向量
是空间的一个基底,则向量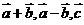 ,也是空间的一个基底。其中正确的命题是(
)
,也是空间的一个基底。其中正确的命题是(
)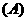 ①②
①② 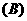 ①③
①③  ②③
②③ 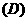 ①②③
①②③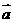 与
与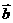 共线,
共线,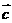 共线,则
共线,则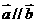 ,则存在唯一的实数
,则存在唯一的实数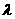 使得
使得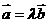 ;
; 为零向量时要注意,B中向量的共线、共面与直线的共线、共面不一样,D中需保证
为零向量时要注意,B中向量的共线、共面与直线的共线、共面不一样,D中需保证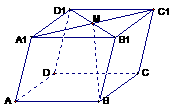 例3.如图:在平行六面体
例3.如图:在平行六面体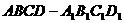 中,
中,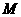 为
为 与
与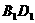 的交点。若
的交点。若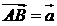 ,
,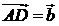 ,
,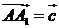 ,则下列向量中与
,则下列向量中与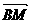 相等的向量是( )
相等的向量是( )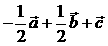
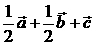
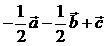
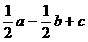
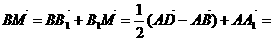
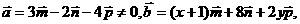 且
且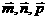 不共面.若
不共面.若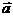 ∥
∥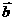 ,求
,求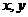 的值.
的值.
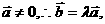 即
即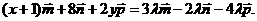
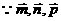 不共面,
不共面,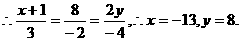
 =(a1,a2,a3),
=(a1,a2,a3),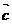 =(4,2,5)
=(4,2,5)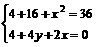

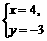 或
或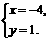 ;
;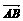 ,
,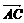 ,(1)求
,(1)求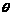 ;(2)若向量k
;(2)若向量k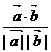 =
=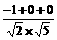
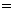 -
-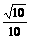 ,
,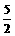 或k=2。
或k=2。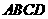 中,截面
中,截面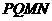 是正方形,则在下列命题中,错误的为
是正方形,则在下列命题中,错误的为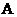 .
. 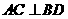
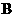 .
.  ∥截面
∥截面 .
. 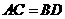
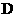 . 异面直线
. 异面直线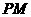 与
与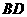 所成的角为
所成的角为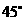
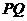 ∥
∥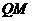 ∥
∥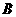 正确;
正确;
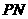 所成的角,故
所成的角,故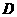 正确;
正确;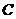 是错误的,故选
是错误的,故选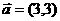 ,
,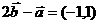 ,
,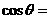 .
.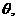 且
且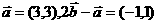 ∴
∴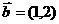 ,则
,则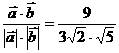 =
=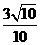 .
.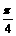 。(1)求x1+y1和x1y1的值;(2)求<
。(1)求x1+y1和x1y1的值;(2)求<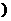 。
。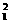 +y
+y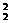 =y
=y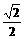
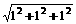 =
=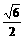 .
.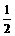 .∴x1y1=
.∴x1y1=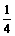 。
。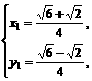 或
或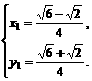 同理可得
同理可得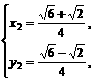 或
或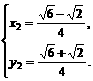
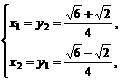 或
或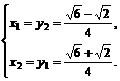
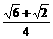 ·
·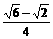 +
+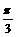 。
。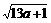 +
+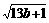 +
+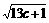 ≤4
≤4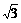 。
。 =(
=(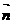 =(1,1,1),
=(1,1,1),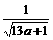 =
=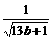 =
=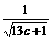 时,即a=b=c=
时,即a=b=c=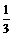 时,取“=”号。
时,取“=”号。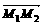 =14。
=14。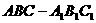 中,
中,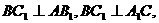 求证:
求证: 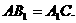
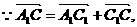
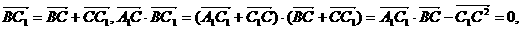
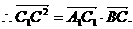
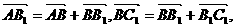
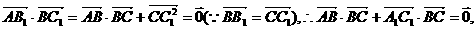
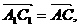
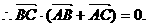
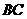 中点,则
中点,则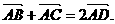
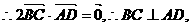
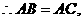 又
又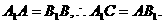
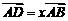 ,
,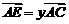 ,
,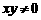 ,则
,则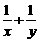 的值为( )
的值为( ) 、
、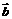 ,在空间任取一点O,作
,在空间任取一点O,作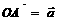 ,
,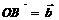 ,则角∠AOB叫做向量
,则角∠AOB叫做向量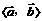
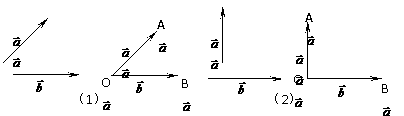
 说明:⑴规定0≤
说明:⑴规定0≤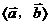 ≤
≤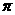 ,因而
,因而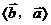 ;
;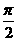 ,则称
,则称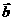 互相垂直,记作
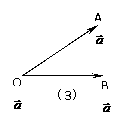
互相垂直,记作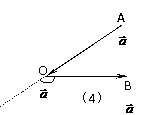 ⑶在表示两个向量的夹角时,要使有向线段的起点重合,注意图(3)、(4)中的两个向量的夹角不同,
⑶在表示两个向量的夹角时,要使有向线段的起点重合,注意图(3)、(4)中的两个向量的夹角不同,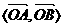 ,
,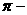
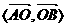 ,
,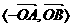 =
=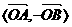 =
=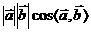 叫做向量
叫做向量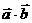 。
。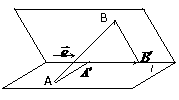 即
即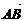
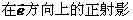 :
: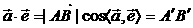

 ⑴
⑴ 。
⑴
。
⑴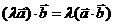

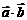 =0
⑵
=0
⑵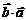
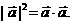 ⑶
⑶