9.已知x，y满足约束条件则z＝的最小值为

A. 　　　　　　　　　　　　　　　　　B.　

C.4　 　　　　　　　　　　　　　　　　　D.－

8.有下列命题：

①函数f(x)＝sin x+(x∈(0，π))的最小值是2；

②在△ABC中，若sin 2A＝sin 2B，则△ABC是等腰三角形或直角三角形；

③如果正实数a，b，c满足a+b＞c，则+＞；

④如果y＝f(x)是可导函数，则f′(x₀)＝0是函数y＝f(x)在x＝x₀处取得极值的必要不充分条件.

其中正确的命题是

A.①②③④　 　　　　　　　　　　　　　B.①④　

C.②③④ 　　　　　　　　　　　　　　D.②③

7.已知f(x)＝1+log₂x(1≤x≤4)，则g(x)＝f(x²)的最大值为

A.1　 　　　　　　　　　　　　　　　B.3　

C.5 　　　　　　　　　　　　　　　　D.9

6.已知a，b为空间两条异面直线，A是直线a，b外一点，则经过A点与两条异面直线a，b都相交的直线的可能情况为

A.至多有一条 　　　　　　　　　　　　B.至少有一条

C.有且仅有一条 　　　　　　　　　　　D.有无数条

5.设F为抛物线y²＝4x的焦点，△ABC的三个顶点都在此抛物线上，且++＝0，则||+||+||等于

A.9　 　　　　　　B.6　 　　　　　　　C.4　 　　　　　　D.3

4.在等差数列{a_n}中，若a₁+a₄+a₇＝39，a₃+a₆+a₉＝27，则数列{a_n}的前9项之和S₉等于

A.66　 　　　　　B.99 　　　　　　　C.144　 　　　　　D.297

3.已知(x－)⁸展开式中的常数项为1120，其中实数a是常数，则展开式中各项系数的和为

A.2⁸　 　　　　　　B.3⁸　 　　　　　　C.1或3⁸ 　　　　D.1或2⁸

2.z∈C，若|z|－＝1－2i，则的值是

A.－2　　　B.－2i　　　C.2　　　D.2i

1.若集合A＝{x|＜0}，B＝{x|x－2＜2}，则“m∈A”是“m∈B”的

A.充分不必要条件　　　　　 B.必要不充分条件

C.充要条件　 　　　　　　　　　　　　D.既不充分也不必要条件

19.(本小题满分12分)

某出版社准备举行一次高中数学新教材研讨会，以征求对新教材的使用意见.邀请50名使用不同版本教材的一线教师参加，使用不同版本教材的教师人数如下表所示：

(I)　　　 从这50名见识中随即选出2名见识发言，求两人所用教材版本相同概率；

(II)　　 若从使用人教版奇偶才的教师中选出2名发言，设使用任教A版的教师人数为 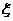，求随机变量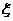的分布列的数学期望.

(20)　 (本小题满分12分)

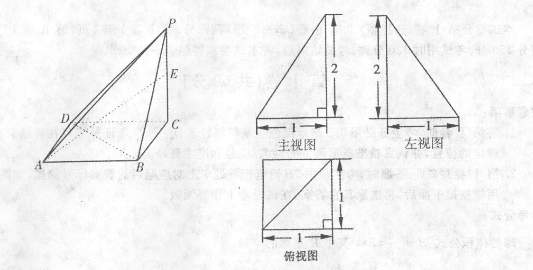
已知一四棱锥P-ABCD的三视图如下，E是则棱PC上的动点.

(I)　　　　　　 求四棱锥P-ABCD的体积;

(II)　　　　 不论点E在何位置，是否都又 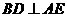?证明你的结论；

(III)　　　 若E点为PC的中点，求二面角D-AE-B的大小.

(21)　 (本小题满分12分)

已知离心率为 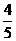的椭圆的中心在远点，焦点在　 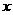轴上.双曲线以椭圆的长轴为实轴，短轴为虚轴，且焦距为

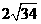
(I)　　　　　　 求椭圆及双曲线的方程；

(II)　　　　 设椭圆的左、右定点分别为A、B，在第二象限内取双曲线上一点P，连接BP交椭圆于点M，连接PA并延长交椭圆于点N，若 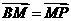求四边形ANBM的面积.

(22)　 (本小题满分14分)

已知 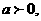函数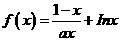

(I)　　　　　　 试问 在定义域上能否是单调函数？请说明理由；

(II)　　　　 若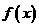在区间 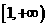上是单调递增函数，试求实数 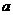的取值范围；

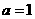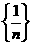(III)　　　 当 时，设数列 的前 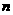项和为　 求证

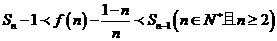
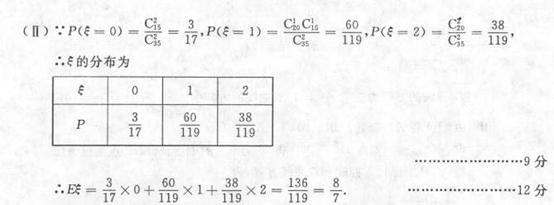
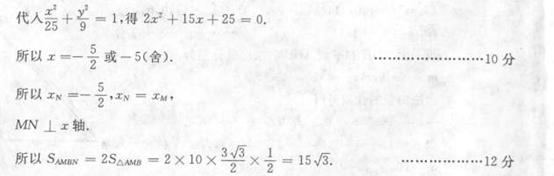
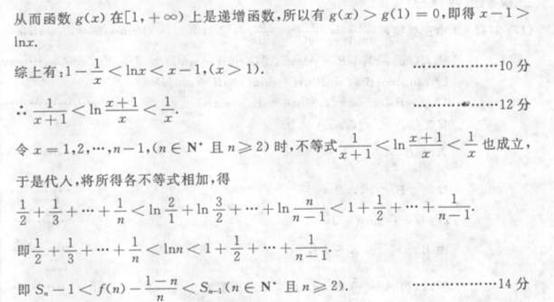
本资料由《七彩教育网》 提供！