0 52430 52438 52444 52448 52454 52456 52460 52466 52468 52474 52480 52484 52486 52490 52496 52498 52504 52508 52510 52514 52516 52520 52522 52524 52525 52526 52528 52529 52530 52532 52534 52538 52540 52544 52546 52550 52556 52558 52564 52568 52570 52574 52580 52586 52588 52594 52598 52600 52606 52610 52616 52624 447348
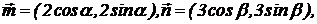 若
若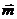 与
与 的夹角为
的夹角为 ,则直线
,则直线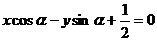 与圆
与圆 的位置关系是( )
的位置关系是( )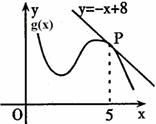 A.相交但不过圆心
B.相交过圆心 C.相切 D.相离
A.相交但不过圆心
B.相交过圆心 C.相切 D.相离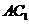 的棱长为
的棱长为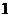 ,过点
,过点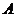 作平面
作平面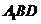 的垂线,垂足为点
的垂线,垂足为点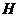 , 则以下命题中,错误的命题是( )
, 则以下命题中,错误的命题是( )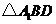 的垂心 B.
的垂心 B. 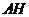 垂直平面
垂直平面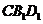
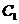 D.直线
D.直线 所成角为
所成角为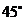
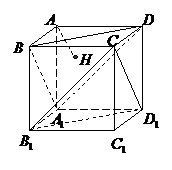 则数表中的2008出现在第
则数表中的2008出现在第 行.
行. 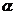 、
、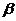 为锐角a=sin(
为锐角a=sin(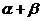 ),b=
),b=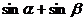 ,则a、b之间关系为
,则a、b之间关系为  若函数
若函数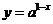
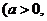 且
且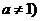 ,图象恒过定点A,又点A在直线
,图象恒过定点A,又点A在直线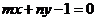 上,若
上,若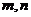 是正数,则
是正数,则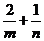 的最小值是
.
的最小值是
.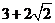
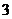 B.
B.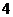 C.
C.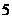 D.
D.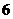
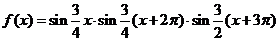 在区间
在区间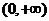 内的全部极值点按从小到大的顺序排成数列
内的全部极值点按从小到大的顺序排成数列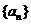 ,
,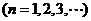 .
.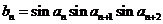 ,求证:
,求证: ,
,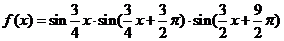
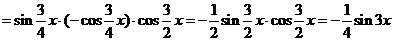
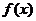 的极值点为
的极值点为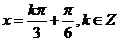 ,从而它在区间
,从而它在区间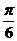 为首项,
为首项,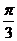 为公差的等差数列,
为公差的等差数列,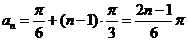 ,
,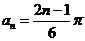 知对任意正整数
知对任意正整数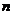 ,
,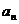 都不是
都不是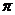 的整数倍,
的整数倍,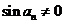 ,从而
,从而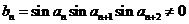
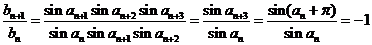
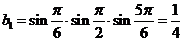 ,
,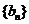 是以
是以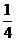 为首项,
为首项,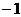 为公比的等比数列。 ∴
为公比的等比数列。 ∴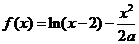 (
(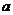 为常数且
为常数且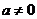 )
)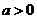 时,求
时,求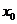 处取得极值,且
处取得极值,且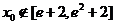 ,而
,而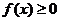 在
在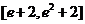 上恒成立,求实数
上恒成立,求实数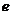 为自然对数的底数)
为自然对数的底数)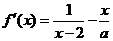 ……………………(1分)
……………………(1分)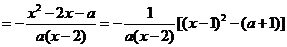
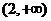 ,所以
,所以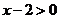
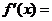
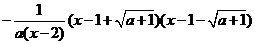
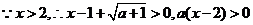
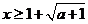 时,
时,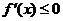 ,
,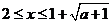 时,
时,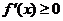 ,
,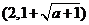
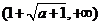 …………………(6分)
…………………(6分)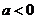 时,
时,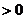 ,
,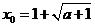
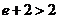 ,所以
,所以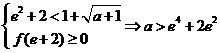 ………………………………………(9分)
………………………………………(9分)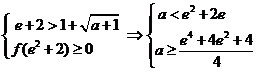 无解 ……………………(13分)
无解 ……………………(13分)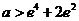 …………………………(14分)
…………………………(14分)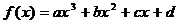 是定义在R上的函数,它在
是定义在R上的函数,它在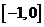 和
和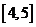 上有相同的单调性,在
上有相同的单调性,在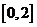 和
和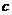 的值;
的值;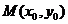 ,使得
,使得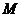 的切线斜率为
的切线斜率为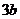 ?若存在,求出
?若存在,求出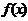 的图象交
的图象交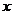 轴于
轴于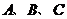 三点,且
三点,且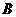 的坐标为
的坐标为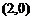 ,求线段
,求线段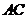 的长度
的长度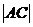 的取值范围.
的取值范围.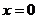 是
是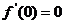 ,即
,即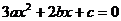 的一个解,所以
的一个解,所以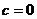 .
.
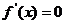 在
在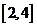 上必有一根.又
上必有一根.又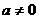 ,易知方程
,易知方程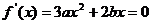 一根为
一根为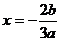 ,所以
,所以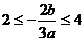 ,∴
,∴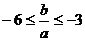
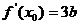 ,即
,即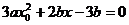 有解.而
有解.而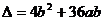 =
=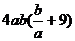 ,因为
,因为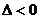 ,与
,与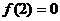 ,又
,又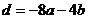 ,
,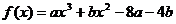 =
=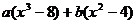
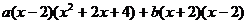 =
=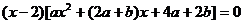 ,
,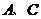 两点的横坐标
两点的横坐标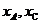 就是方程
就是方程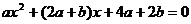 的两根,所以
的两根,所以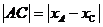 =
=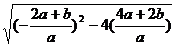 =
=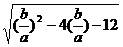 =
=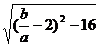 ,
,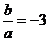 时,
时, ;当
;当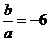 时,
时,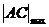 =
=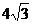 .
.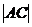 的取值范围是
的取值范围是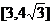 .
.
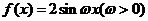 在区间
在区间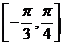 上的最小值是
上的最小值是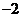 ,则
,则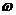 的最小值等于 ( B )
的最小值等于 ( B )
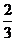 B.
B.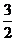 C.2 D.3
C.2 D.3 (
( 的正整数),如果在
的正整数),如果在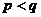 时有
时有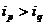 ,则称
,则称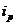 与
与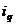 是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为此数组的“逆序数”.若各数互不相等的正数数组
是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为此数组的“逆序数”.若各数互不相等的正数数组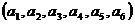 的“逆序数”是2,则
的“逆序数”是2,则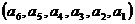 的“逆序数”是 .
13
的“逆序数”是 .
13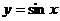 的定义域为
的定义域为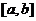 ,值域为
,值域为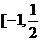 ],则
],则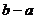 的最大值和最小值之和为B
的最大值和最小值之和为B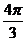 B.2
B.2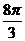 D.
D.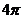
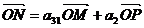 (直线MP不过点O),则S32等于 ( B )
(直线MP不过点O),则S32等于 ( B )