20.(12分)已知函数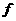 (
(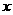 ) = a
) = a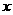 3 + b
3 + b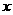 2 + c (a,b,c∈R,a≠0) 的图像过点P( -1, 2 ),且在点P处的切线与直线
2 + c (a,b,c∈R,a≠0) 的图像过点P( -1, 2 ),且在点P处的切线与直线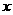 - 3
- 3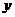 = 0垂直.
= 0垂直.
(1)若c = 0试求函数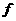 (
(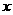 ) 的单调区间;
) 的单调区间;
(2)若 a > 0 , b > 0且 ( - , m ) , ( n ,+
, m ) , ( n ,+ )是
)是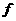 (
(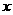 ) 的单调递增区间,试求n - m的范围.
) 的单调递增区间,试求n - m的范围.
|
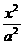 +
+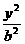 = 1( a > b > 0 )的左焦点为F,上顶点为A.过A做直线
= 1( a > b > 0 )的左焦点为F,上顶点为A.过A做直线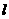
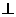 AF,
AF,
l分别交椭圆和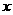 轴正半轴于P、Q两点,若P分AQ所成的比为8∶5.
轴正半轴于P、Q两点,若P分AQ所成的比为8∶5.
(1)求椭圆的离心率;
(2)若过A、Q、F三点的圆恰好与直线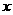 +
+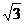
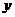 + 3 = 0相切,求椭圆方程.
+ 3 = 0相切,求椭圆方程.
22(14分)
已知Pn( an ,bn )( n∈N*
)都在直线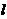 ∶y = 2
∶y = 2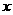 + 2上,P1为
+ 2上,P1为 直线
直线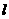 与
与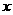 轴的交点,数列|an|为等差数列,公差为1.
轴的交点,数列|an|为等差数列,公差为1.
(1)求数列{an}、{bn}的通项公式;
(2)若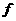 (n) =
(n) =  是否存在
是否存在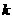 ∈N*,使得
∈N*,使得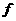 (
(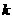 +5)=2
+5)=2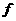 (
(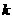 )-2成立?
)-2成立?
若存在,求出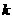 值;若不存在,说明理由;
值;若不存在,说明理由;
(3)求证: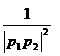 +
+ 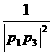 + … +
+ … + 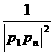 <
< 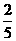 ,(n ≥ 2,n ∈ N
,(n ≥ 2,n ∈ N )
)
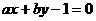 (
(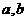 不全为
不全为 )与圆
)与圆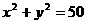 有公共点,且公共点的横、纵坐标均为整数,那么这样的直线有
( )
有公共点,且公共点的横、纵坐标均为整数,那么这样的直线有
( )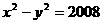 的左、右顶点分别为
的左、右顶点分别为 、
、 ,
,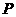 为其右支上一点,且
为其右支上一点,且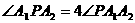 ,则
,则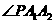 等于
(
)
等于
(
) C.
C.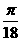 D.
D.
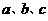 是常数,则“
是常数,则“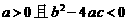 ”是“对任意
”是“对任意 ,有
,有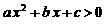 ”的 ( )
”的 ( ) 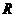 ,若甲地位于北纬
,若甲地位于北纬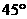 东经
东经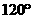 ,乙地位于南纬
,乙地位于南纬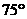 东经
东经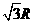 B.
B.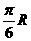 C.
C.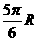 D.
D.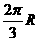
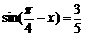 ,则
,则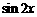 的值为
( )
的值为
( )
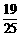 B.
B.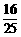 C.
C.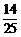 D.
D.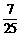
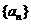 中,若
中,若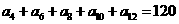 ,则
,则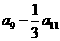 的值为 ( )
的值为 ( ) 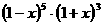 的展开式中
的展开式中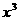 的系数为
( )
的系数为
( )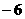 B.
B.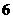 C.
C.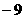 D.
D.
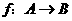 ,其中
,其中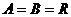 ,对应法则
,对应法则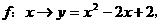 若对实数
若对实数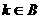 ,在集合A中不存在原象,则
,在集合A中不存在原象,则 的取值范围是
( )
的取值范围是
( )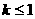 B.
B.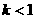 C.
C.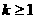 D.
D.