0 160818 160826 160832 160836 160842 160844 160848 160854 160856 160862 160868 160872 160874 160878 160884 160886 160892 160896 160898 160902 160904 160908 160910 160912 160913 160914 160916 160917 160918 160920 160922 160926 160928 160932 160934 160938 160944 160946 160952 160956 160958 160962 160968 160974 160976 160982 160986 160988 160994 160998 161004 161012 447348
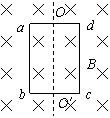
 A.磁通量和感应电动势都在变大
A.磁通量和感应电动势都在变大 A.穿过线圈的磁通量变化率为零
A.穿过线圈的磁通量变化率为零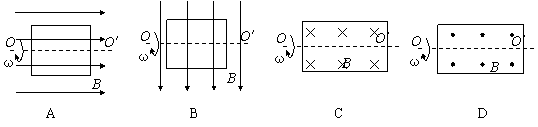
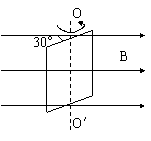
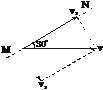
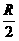 ,OP=
,OP=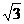 R.求玻璃材料的折射率.
R.求玻璃材料的折射率.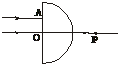
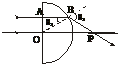
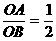 (3分)
(3分)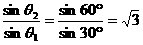 =1.73. (3分)
=1.73. (3分)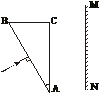

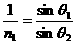 (2分)
(2分)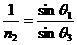 (2分)
(2分)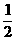 n1 (1分)
n1 (1分)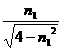 (1分)
(1分)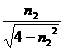 (1分)
(1分)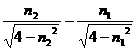 ). (2分)
). (2分)
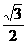 v. (3分)
v. (3分)