0 160070 160078 160084 160088 160094 160096 160100 160106 160108 160114 160120 160124 160126 160130 160136 160138 160144 160148 160150 160154 160156 160160 160162 160164 160165 160166 160168 160169 160170 160172 160174 160178 160180 160184 160186 160190 160196 160198 160204 160208 160210 160214 160220 160226 160228 160234 160238 160240 160246 160250 160256 160264 447348
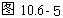
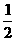 个周期,滞后
个周期,滞后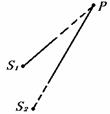
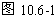
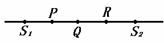
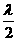 (n=0、1、2、3…)时,为反相振动,叠加结果是两数之差,即振动减弱,是减弱点.由此看来,加强点和减弱点只与位置有关,不随时间变化.正因为不随时间变化,才能被观察到,才能形成干涉图样.
(n=0、1、2、3…)时,为反相振动,叠加结果是两数之差,即振动减弱,是减弱点.由此看来,加强点和减弱点只与位置有关,不随时间变化.正因为不随时间变化,才能被观察到,才能形成干涉图样.
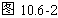

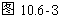
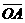 -
-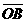 =5m=5·
=5m=5·