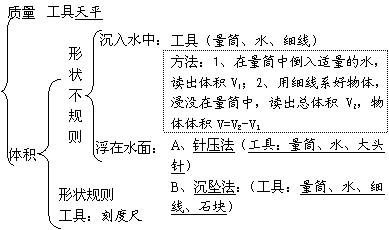
10.4密度的测量
题型一 有关测量物质密度的实验题
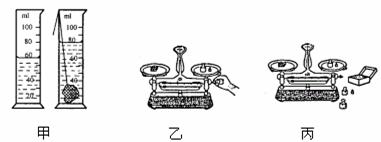
例1 在“用天平和量筒测定固体密度”的实验中,某同学正确测得石块质量为48g,体积如图10-16甲为________cm3,石块的密度是_______________kg/m3 ,图乙是个别同学在实验操作过程中的情况;图丙是部分同学实验结束离开实验室后留下的情景。指出图中违反实验操作规则和实验不规范之处。
图乙:________________________________________________________。
图丙:_________________________________________________________。
|
知识点 用天平和量筒测物质的密度
闯关点拨 从甲图可以看出V水=60mL,水和石块的总体积V总=80mL,则V石=60 mL;利用天平测量质量时,在称量时不能调节平衡螺母,实验完成后应该整理好器材。
答 20 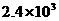 称物体质量时又重新调节平衡螺母 离开实验室前没有把器材整理好
称物体质量时又重新调节平衡螺母 离开实验室前没有把器材整理好
例2 在用天平和量筒测量某种食油的密度时,以下操作步骤中,不必要且不合理的是( )
A.用天平测出空烧杯的质量
B.取适量的油倒入烧杯中,用天平测出杯和油的总质量
C.将烧杯中的油倒入量筒中,测出倒入量筒中的油的体积
D.用天平测出烧杯和剩余油的总质量
知识点 利用等量替代法测物质的密度
闯关点拨 我们在设计实验步骤的时候,必须具有可操作性和科学性,并能力求减少实验的误差。因此,本题就应该先测烧杯和油的总质量,再测出倒出油后的杯子质量,这样两者之差就是倒出油的质量,而此时量筒内油的体积也就是倒出的油体积,有利于减小实验误差,因而用天平测出空烧杯的质量是不必要且不合理的。
答 选A
[变形题] 某班同学收集到一块火山岩标本,他们使用天平、盛水量筒和绳子测火山岩的密度时,出现不规范操作:
(1)用绳子扎住这块火山岩,浸没在量筒的水中测它的体积.
(2)测量过程中观察量筒读数时,视线均与液面边缘相平.
(3)测火山岩体积时发现火山岩吸水性很强.
(4)测完火山岩体积,将其取出立即放在天平的盘中称测量.
上述有些操作会造成测量值偏大或偏小,其中造成测量值偏小的步骤是 .(填序号)
分析 本题所测的石块──火山岩,与平常的石块不同,火山岩质地疏松,吸水性强,在用排水法测它的体积石易造成偏差,这种偏差主要是:(1)对质量测量的偏差.先放入水中测体积后,火山岩吸收了较多的水,再测质量时,火山岩的质量测量值比真实值大;(2)体积测量偏差.当干的火山岩放入水中后吸收了较多水,使得量筒中的水变少,示数增加的值偏少,测量得到的火山岩体积的测量值比真实值小.
解 造成测量值偏小的步骤是(1).
例3 “正北牌”方糖是利用一种白砂糖精制而成的长方形糖块,为了测出它的密度,除了一些方糖外,还有下列器材:天平、量筒、毫米刻度尺、水、白砂糖、小勺、镊子、玻璃棒,利用上述器材可有多种测量方糖密度的方法,请你设计出2种测方糖密度大小的方案.要求:写出方案的设计步骤及所测物理量,并用所测物理量表示方糖的密度.
知识点 用多种方法测物质的密度
闯关点拨 此题是一个开放型试题,在这个实验中,实验原理是相同的,但由于实验方法不同,从而导致结论不同,解题的关键是熟练掌握实验原理和基本仪器的使用.
解 测量方法有以下几种:
方法一:用天平测出3块方糖的质量m,用毫米刻度尺测出其中一块的长a、宽b、高c,则密度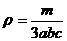 .
.
方法二:用天平测出3块方糖的质量m,向量筒里倒入适量水,记下水的体积V1;把三块方糖放入量筒内的水中,马上读出这时水和方糖的总体积V2,则密度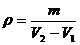 .
.
方法三:用天平测出3块方糖的质量m,向量筒里倒入适量水并放入白砂糖,用玻璃棒搅动制成白砂糖的饱和溶液,记下饱和溶液的体积V1,把3块方糖放入饱和溶液中,记下饱和溶液和方糖的总体积V2.则密度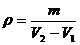 .
.
方法四:用天平测出3块方糖的质量m,再把3块方糖放入量筒里,倒入适量白砂糖埋住方糖,晃动量筒,使白砂糖表面变平,记下白砂糖和方糖的总体积V1;用镊子取出方糖,晃动量筒使白砂糖表面变平,记下白砂糖的体积V2.则密度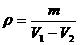 .
.
题型二 测量物质密度的一些特殊方法
例 给你一架无砝码、无游码、已调好的等臂天平和一个量杯、细绳、一些细砂及适量的水(设水的密度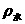 已知)。请你测出一块小矿石的密度要求:
已知)。请你测出一块小矿石的密度要求:
(1)写出实验步骤及要测量的物理量。
(2)推出用所测物理量表达矿石密度的表达式。
知识点 用间接方法测量物质的密度
闯关点拨 测小矿石的密度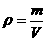 ,需测出小矿石的质量m和体积V。用量筒可测出小矿石体积,小矿石质量如何测得是本题的难点和重点。
,需测出小矿石的质量m和体积V。用量筒可测出小矿石体积,小矿石质量如何测得是本题的难点和重点。
析 根据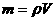 ,对已知密度的物体,如果其体积能够测得,则其质量可求得。在所提供的物体中,只有水的密度已知,其他密度未知,利用量筒和水以及天平,可以间接地测出其他物体的质量。
,对已知密度的物体,如果其体积能够测得,则其质量可求得。在所提供的物体中,只有水的密度已知,其他密度未知,利用量筒和水以及天平,可以间接地测出其他物体的质量。
为了使被测小矿石的质量与量杯中水的质量相等,测量小矿石质量前,需先用一些细砂平衡量杯的质量,即在一盘放空量杯,在另一盘放细砂并调节细砂使天平平衡,再在装细砂的盘中加小矿石,并在量杯中加水,使天平再次平衡,此时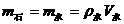 ,读出水的体积即可求得
,读出水的体积即可求得 。
。
答 (1)实验步骤及要测量的物理量:
A.将空量杯放在右盘,在左盘放适量的细砂,使天平平衡;
B.在左盘再放上小矿石,在右盘的空量杯中慢慢加水,直至天平再次平衡;
C.记录下此时量杯中水的体积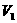 ;
;
D.取下量杯,在杯中装适量的水,记录下此时量杯中水的体积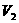 ;
;
E.将小矿石放入量杯中,记录下此时量杯中水面对应的示数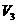 。
。
(2)推导:
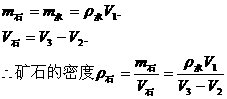
[变形题] 给你一架已调好平衡的天平(配有砝码),和一个盛满水的烧杯,只用这些器材(不使用任何其他辅助工具),测出一包金属颗粒的密度.要求:写出测量步骤和计算该金属颗粒的密度数学表达式.
解 (1)用天平测出金属颗粒的质量m1;
(2)用天平测出盛满水的烧杯的总质量m2;
(3)将这些金属颗粒投入烧杯的水中,待水溢出后,用天平测出烧杯、水和金属颗粒的总质量m3.
(4)金属颗粒的密度: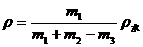 .
.
题型三 利用密度知识解决简单的实际问题
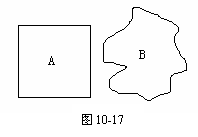 例 如图10-17所示,A、B是从一块厚度均匀的薄铁皮上截下来的两块小铁皮,其中A块是正方形,B块形状不规则.给你刻度尺、天平和砝码,你能否测算出B块铁皮的面积?写出测量步骤并推导出面积的表达式.
例 如图10-17所示,A、B是从一块厚度均匀的薄铁皮上截下来的两块小铁皮,其中A块是正方形,B块形状不规则.给你刻度尺、天平和砝码,你能否测算出B块铁皮的面积?写出测量步骤并推导出面积的表达式.
知识点 用密度知识解决简单的问题
闯关点拨 由于两块铁皮的厚度相同,故它们的面积与体积成正比,即SA∶SB=VA∶VB,而它们的材料又相同,则体积又与质量成正比,由此可得SA∶SB= mA∶mB.所以只要测出mA、mB和SB即可求得B的面积.
答 (1)用刻度尺测出A的边长为a;(2)用天平分别测出A、B的质量为mA、mB.
B的面积: .
.
10.3 密度
题型一 理解密度的概念,理解密度是物质的一种特性
例1 由密度的概念及公式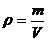 ,可以判定对于同一种物质( )
,可以判定对于同一种物质( )
A.密度是一样的 B.体积越小,密度越大
C.质量越大,密度越大 D.体积越大,密度越大
知识点 理解密度的物理意义
闯关点拨 物理学中的定义式与数学中的函数式是有区别的,定义式中各量之间除了数量关系外,更重要的是有其特定的物理含义.因此,对于物理量的定义式不能从中简单地得出谁跟谁成正比,谁跟谁成反比的结论.
分析和解 密度是由物质种类决定的,与物体的质量、体积无关.因而B、C、D选项都是错误的.对于某中物质组成的物体,其密度是一个定值,质量跟体积的比值等于密度,因而也是一个定值.
答 选A
例2 关于密度的概念下列说法正确的是( )
A.同一种物质它的密度跟其质量成正比,跟其体积成反比
B.把一铁块压成铁片,它们的密度就小了
C.一种固体和一种液体,它们的质量相等,体积相等,则它们的密度也相等
D.质量相等的两种物质,密度大的体积也大
知识点 知道密度是物质的一种特性
闯关点拨 密度是物质的一种特性,对于同种物质,无论质量和体积怎样改变,物质的密度始终是不变的,所以A、B是错误的。质量相等的不同物质,密度大的体积反而小,所以D也是错误的。一般来讲,不同物质的密度是不同的,但并不等于密度相同的就一定是同种物质,C所述的结论是正确的,因为按密度的概念,可以判断两种物质的密度的确相等。
答 选C
[变形题] 将一块质量分布均匀的砖分割成体积大小不同的两部分,则( ).
A.体积大的密度一定大 B.体积小的密度一定大
C.两者的密度一定相等 D.两者的密度一定不相等
答 选C
题型二 通过实验探究,知道物质的质量与体积的关系,会用图像的方法解决物理问题
例 为了研究物质的某种特性,某同学分别用甲、乙两种不同的液体做实验,实验时,他用量筒和天平分别测出甲(或乙)液体在不同体积时的质量,下表记录的是实验测得的数据及求得的质量跟体积的比值。
|
物质 |
实验次数 |
体积(c㎡) |
质量(g) |
质量/体积(g/c㎡) |
|
甲 |
1 |
10 |
18 |
1.8 |
|
2 |
20 |
36 |
1.8 |
|
|
3 |
30 |
54 |
1.8 |
|
|
乙 |
4 |
10 |
8 |
0.80 |
|
5 |
20 |
16 |
0.80 |
|
|
6 |
30 |
24 |
0.80 |
(1)分析上表中的实验次数1与2(2与3、1与3)或4与5(5与6、4与6)的体积及质量变化的倍数关系,可归纳出的结论是____________________
(2)分析上表中实验次数___________,可归纳出的结论是相同体积的甲、乙两种液体,它们的质量是不相同的。
(3)分析上表中甲、乙两种液体的质量与体积的比值关系,可归纳出的结论是___________
知识点 通过实验探究,理解密度的概念
闯关点拨 本题引导同学们通过分析研究物质的某种特性的实验数据,探究和归纳知识。应注意在分析数据时明确:对同种物质,在体积改变时,质量和体积比值特点;对不同物质在体积相同的情况下,质量与体积的比值特点,不难得出结论。
答 (1)甲(或乙)液体的质量与体积成正比。(2)1与4(2与5、3与6)在相同体积时的质量关系。(3)甲(或乙)液体,它的质量与体积的比值是一个确定的值;甲与乙液体,它们的质量与体积的比值是不同的。
题型三 能较灵活地利用密度公式及其变形公式计算物质的密度及物体的质量、体积
例1 一个瓶子的质量为20g,装满水时,用天平测得总质量为120g,若用这个瓶子装密度为1.8×103kg/m3的硫酸最多可装多少千克?
知识点 利用密度公式及其变形公式进行计算
闯关点拨 要求瓶子最多可以装多少硫酸,硫酸的密度是已知的,只需知道硫酸的体积,而硫酸的体积等于瓶子容积,求出瓶子的容积是关键,根据装满水时水的质量和水的密度求出瓶的容积,就可求出最多能多少千克硫酸了。
解 解法一:(分步求解是最基本的解题方法)
根据水的质量m水=120g-20g=100g=0.1kg和水的密度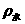 =1.0×103 kg/m3求出水的体积为:
=1.0×103 kg/m3求出水的体积为: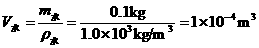
则硫酸的体积为V硫酸=V容=V水
m硫酸=ρ硫酸·V硫酸=1.8×103 kg/m3×1×10-4m3 =0.18kg
解法二:掌握了密度知识比例关系,也可以用比例方法解题.
∵V硫酸=V水
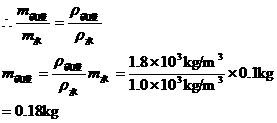
例2 一铁球的质量是2.2kg,体积是0.4×10-3m3,试鉴定此球是空心的还是实心的。
(ρ铁=7.9g/cm3)
知识点 应用密度知识解决实际问题
闯关点拨 鉴定球是否空心有三种方法。方法一:比较密度,假设球是实心的,用求出的铁球密度与铁的已知密度相比,若相等则是实心的,若小于铁的密度则是空心的;方法二:比较质量假设球是实心的,求出铁球的质量与题目所给的质量相比,若相等则是实心,若大于题目所给的质量则是空心的;方法三:比较体积求出铁球中铁的体积与题所给体积相比,若相同则是实心的,若小于题目所给的体积则是空心的。
解 方法一:铁球密度ρ=m/V=2.2kg/0.4×10-3m3=5.5×103kg/m3
因为5.5×103kg/m3<7.9×103kg/m3,所以是空心的。
方法二:若铁球是实心的,则铁球的质量m=ρV=7.9×103kg/m3×0.4×10-3m3=3.16kg
因为3.16kg>2.2kg,所以球是空心的。
方法三:因为铁的体积:V=m/ρ=2.2kg/7.9×103kg·m-3=0.28×10-3m3<0.4×10-3m3
所以铁球是空心的。
[变形题] 用相同质量的铝和铜制成体积相等的球,已知ρ铝=2.7×103kg/m3,ρ铜=8.9×103kg/m3,则下列说法正确的是( )
A.铜球不可能是实心的 B.铝球是实心的,铜球可能是实心的
C.铜球是空心的,铝球一定是空心的 D.铝球和铜球都是实心的
解 根据密度公式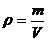 ,有
,有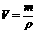 ,因铝球和铜球的质量相同,但ρ铝<ρ铜,故V铝>V铜,即实心铝球的体积必然大于实心铜球的体积,而体重要求铝球和铜球的体积要相等,在铝球体积无法减小的前提下,只有增大铜球的体积,才有可能使两球的体积相等,故铜球只能制成空心的,即铜球不可能是实心的,因此A选项正确,可排除B、D选项;至于C选项可以这样来分析──当铜球是空心的时候,铝球有两种可能,要么是实心,要么是空心,即铝球可能而并非一定是空心的,故排除C选项
,因铝球和铜球的质量相同,但ρ铝<ρ铜,故V铝>V铜,即实心铝球的体积必然大于实心铜球的体积,而体重要求铝球和铜球的体积要相等,在铝球体积无法减小的前提下,只有增大铜球的体积,才有可能使两球的体积相等,故铜球只能制成空心的,即铜球不可能是实心的,因此A选项正确,可排除B、D选项;至于C选项可以这样来分析──当铜球是空心的时候,铝球有两种可能,要么是实心,要么是空心,即铝球可能而并非一定是空心的,故排除C选项
答 选A
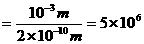 (个),
(个), 有天平、烧杯、水,请测出一杯牛奶的密度(缺量筒)
有天平、烧杯、水,请测出一杯牛奶的密度(缺量筒)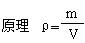 测固体的密度:
测固体的密度: