摘要:(Ⅰ)已知函数:求函数的最小值; (Ⅱ)证明:, (Ⅲ)定理:若 均为正数,则有 成立 (其中.请你构造一个函数.证明: 当均为正数时.. 解:(Ⅰ)令得-2分 当时. 故在上递减. 当故在上递增.所以.当时.的最小值为.-.4分 (Ⅱ)由.有 即 故 .---------------5分 (Ⅲ)证明:要证: 只要证: 设-------7分 则 令得--------------------.8分 当时. 故上递减.类似地可证递增 所以的最小值为------10分 而 = == 由定理知: 故 故 即: .----------..14分
网址:http://m.1010jiajiao.com/timu3_id_540099[举报]
已知函数 .
.
(Ⅰ)求函数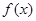 的最小值;
的最小值;
(Ⅱ)求证: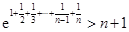
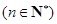 ;
;
(Ⅲ)对于函数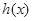 与
与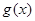 定义域上的任意实数
定义域上的任意实数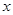 ,若存在常数
,若存在常数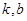 ,使得
,使得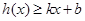 和
和 都成立,则称直线
都成立,则称直线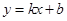 为函数
为函数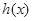 与
与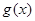 的“分界线”.设函数
的“分界线”.设函数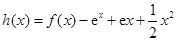 ,
,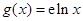 ,
,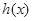 与
与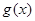 是否存在“分界线”?若存在,求出
是否存在“分界线”?若存在,求出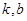 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看习题详情和答案>>
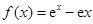 .
. 的最小值;
的最小值;
 ;
;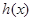 与
与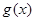 定义域上的任意实数
定义域上的任意实数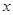 ,若存在常数
,若存在常数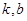 ,使得
,使得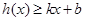 和
和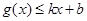 都成立,则称直线
都成立,则称直线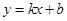 为函数
为函数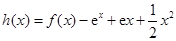 ,
,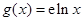 ,
,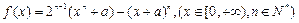 求函数
求函数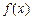 的最小值;
的最小值;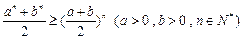 ;
;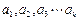 均为正数,则有
均为正数,则有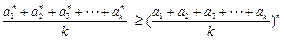 成立(其中
成立(其中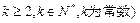 .请你构造一个函数
.请你构造一个函数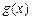 ,证明:
,证明: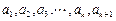 均为正数时,
均为正数时,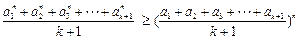 .
.