摘要：4．注重数学思想方法的教学 ①．数形结合的思想方法. 由于向量本身具有代数形式和几何形式双重身份.所以在向量知识的整个学习过程中.都体现了数形结合的思想方法.在解决问题过程中要形成见数思形.以形助数的思维习惯.以加深理解知识要点.增强应用意识. ②．化归转化的思想方法. 向量的夹角.平行.垂直等关系的研究均可化归为对应向量或向量坐标的运算问题,三角形形状的判定可化归为相应向量的数量积问题,向量的数量积公式.沟通了向量与实数间的转化关系,一些实际问题也可以运用向量知识去解决. ③．分类讨论的思想方法. 如向量可分为共线向量与不共线向量,平行向量可分为同向向量和反向向量,向量在方向上的投影随着它们之间的夹角的不同.有正数.负数和零三种情形,定比分点公式中的随分点P的位置不同.可以大于零.也可以小于零.
网址：http://m.1010jiajiao.com/timu3_id_537018[举报]
（2013•福建）当x∈R，|x|＜1时，有如下表达式：1+x+x2+…+xn+…=
两边同时积分得：
1dx+
xdx+
x2dx+…
xndx+…=
dx
从而得到如下等式：1×
+
×(
)2+
×(
)3+…+
×(
)n+1+…=ln2．
请根据以上材料所蕴含的数学思想方法，计算：
×
+
×(
)2+
×(
)3+…+
×(
)n+1=
[(
)n+1-1]
[(
)n+1-1]．
查看习题详情和答案>>
| 1 |
| 1-x |
两边同时积分得：
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| 1 |
| 1-x |
从而得到如下等式：1×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| 2 |
请根据以上材料所蕴含的数学思想方法，计算：
| C | 0 n |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 1 n |
| 1 |
| 2 |
| 1 |
| 3 |
| C | 2 n |
| 1 |
| 2 |
| 1 |
| n+1 |
| C | n n |
| 1 |
| 2 |
| 1 |
| n+1 |
| 3 |
| 2 |
| 1 |
| n+1 |
| 3 |
| 2 |
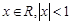时，有如下表达式:
时，有如下表达式： 
两边同时积分得：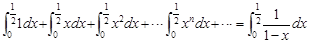
（a>b>0）,点
在椭圆上。
的定义域为
且
，对任意
都有
满足
N
.证明函数
的通项公式;令
N
时,
.