题目内容
已知函数![]() 的定义域为
的定义域为![]() 且
且![]() ,对任意
,对任意![]() 都有
都有![]()
![]()
数列![]() 满足
满足![]() N
N![]() .证明函数
.证明函数![]() 是奇函数;求数列
是奇函数;求数列![]() 的通项公式;令
的通项公式;令![]() N
N![]() , 证明:当
, 证明:当![]() 时,
时,![]() .
.
(本小题主要考查函数、数列、不等式等知识, 考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识)
【解析】(1)由于对任意![]() ,都有
,都有![]() ,
,
令![]() ,得
,得![]() ,解得
,解得![]() . …… 1分
. …… 1分
令![]() ,得
,得![]() ,∵
,∵![]() ,
,
∴![]() ,即
,即![]() .…… 2分 ∴函数
.…… 2分 ∴函数![]() 是奇函数. …… 3分
是奇函数. …… 3分
(2)解:先用数学归纳法证明![]() .①当
.①当![]() 时,
时,![]() ,得
,得![]() , 结论成立.
, 结论成立.
②假设![]() 时, 结论成立, 即
时, 结论成立, 即![]() ,当
,当![]() 时, 由于
时, 由于![]() ,
, ![]() ,
,
又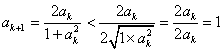 .∴
.∴![]() .即
.即![]() 时, 结论也成立.
时, 结论也成立.
由①②知对任意![]() N
N![]() ,
, ![]() .…… 4分
.…… 4分
求数列![]() 的通项公式提供下面两种方法.
的通项公式提供下面两种方法.
法1: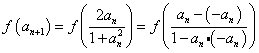
![]() .…………… 5分
.…………… 5分
∵函数![]() 是奇函数, ∴
是奇函数, ∴![]() . ∴
. ∴![]()
![]() . …… 6分
. …… 6分
∴数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
∴数列![]() 的通项公式为
的通项公式为![]() . ……… 7分
. ……… 7分
法2: ∵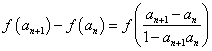 …… 5分
…… 5分
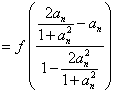
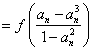
![]()
![]() , ∴
, ∴![]()
![]() .… 6分
.… 6分
∴数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
∴数列![]() 的通项公式为
的通项公式为![]() .………… 7分
.………… 7分
(3)证法1:由(2)知![]() ,∵
,∵![]()
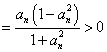 ,
,
∴![]() . … 8分∴
. … 8分∴![]() N
N![]() ,且
,且![]()
∴![]() N
N![]() ,且
,且![]() .… 9分当
.… 9分当![]() 且
且![]() N
N![]() 时,
时,
![]()
![]() …… 10分
…… 10分
![]() …… 11分
…… 11分 ![]()
![]() .
.
∴![]() . … 12分∵
. … 12分∵![]() ,∴当
,∴当![]() 时,
时,![]() .… 13分
.… 13分
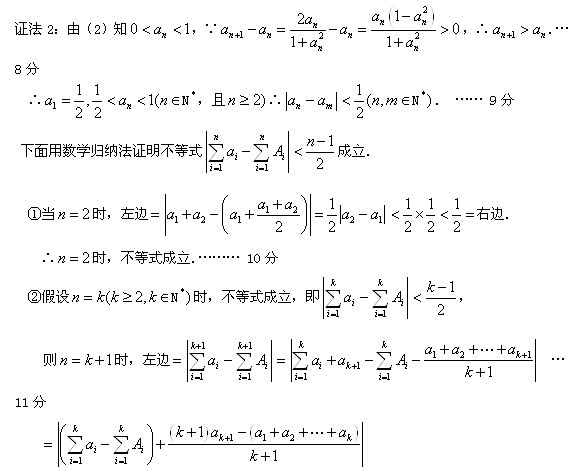 ∴当
∴当![]() 时,
时,![]() . 14分
. 14分
![]() ………… 12分
………… 12分
![]()
![]()
![]()
![]()
![]()
![]()
![]() 右边.……… 13 ∴
右边.……… 13 ∴![]() 时,不等式也成立.
时,不等式也成立.
由①②知,当![]() 时,
时,![]() 成立.………… 14分
成立.………… 14分
证法3:由(2)知![]() ,故对
,故对![]() ,有
,有
![]() .… 8分
.… 8分


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
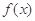 的定义域为
的定义域为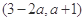 ,且
,且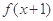 为偶函数,则实数
为偶函数,则实数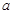 的值可以是( )
的值可以是( )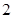 B.
B.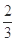 C.
C.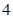 D.
D.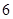
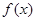 的定义域为
的定义域为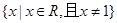 , 且
, 且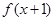 奇函数.当
奇函数.当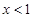 时,
时, 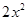 -
-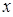 -1,那么函数
-1,那么函数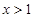 时,
时, B.
B.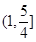 C.
C.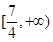 D.
D.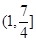
 的定义域为
的定义域为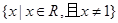 , 且
, 且 奇函数.当
奇函数.当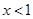 时,
时, 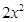 -
-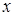 -1,那么函数
-1,那么函数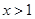 时,
时, 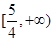 B.
B. C.
C. D.
D.
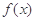 的定义域为
的定义域为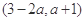 ,且
,且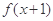 为偶函数,则实数
为偶函数,则实数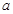 的值可以是( )
的值可以是( )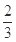 B.
B.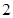 C.
C.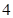 D.
D.