摘要:3.抛物线 (1)抛物线的概念 平面内与一定点F和一条定直线l的距离相等的点的轨迹叫做抛物线(定点F不在定直线l上).定点F叫做抛物线的焦点.定直线l叫做抛物线的准线. 方程叫做抛物线的标准方程. 注意:它表示的抛物线的焦点在x轴的正半轴上.焦点坐标是F(,0).它的准线方程是 , (2)抛物线的性质 一条抛物线.由于它在坐标系的位置不同.方程也不同.有四种不同的情况.所以抛物线的标准方程还有其他几种形式:...这四种抛物线的图形.标准方程.焦点坐标以及准线方程如下表: 标准方程 图形 焦点坐标 准线方程 范围 对称性 轴 轴 轴 轴 顶点 离心率 说明:(1)通径:过抛物线的焦点且垂直于对称轴的弦称为通径,(2)抛物线的几何性质的特点:有一个顶点.一个焦点.一条准线.一条对称轴.无对称中心.没有渐近线,(3)注意强调的几何意义:是焦点到准线的距离.
网址:http://m.1010jiajiao.com/timu3_id_536830[举报]
双曲线![]() 的一条渐近线为
的一条渐近线为![]() ,由方程组
,由方程组 ,消去y,得
,消去y,得![]() 有唯一解,所以△=
有唯一解,所以△=![]() ,
,
所以![]() ,
,![]() ,故选D. w.w.w.k.s.5.u.c.o.m
,故选D. w.w.w.k.s.5.u.c.o.m ![]()
![]()
答案:D.
【命题立意】:本题考查了双曲线的渐近线的方程和离心率的概念,以及直线与抛物线的位置关系,只有一个公共点,则解方程组有唯一解.本题较好地考查了基本概念基本方法和基本技能.
查看习题详情和答案>>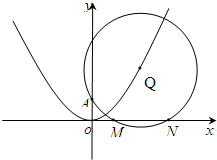 已知⊙Q过定点A(0,p)(p>0),圆心Q在抛物线x2=2py上运动,MN为圆Q在x轴上所截得的弦.
已知⊙Q过定点A(0,p)(p>0),圆心Q在抛物线x2=2py上运动,MN为圆Q在x轴上所截得的弦.