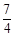题目内容
已知F是抛物线y=
x2的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是( )
| 1 |
| 4 |
A、x2=y-
| ||
B、x2=2y-
| ||
| C、x2=2y-1 | ||
| D、x2=2y-2 |
分析:先把抛物线飞整理成标准方程,然后求得抛物线的焦点,设出P和Q的坐标,然后利用F和Q的坐标表示出P的坐标,进而利用抛物线方程的关系求得x和y的关系及Q的轨迹方程.
解答:解:抛物线y=
x2的标准方程是x2=4y,故F(0,1).
设P(x0,y0),PF的中点Q(x,y)
∴
?
∴x02=4y0,即x2=2y-1.
故选C
| 1 |
| 4 |
设P(x0,y0),PF的中点Q(x,y)
∴
|
|
∴x02=4y0,即x2=2y-1.
故选C
点评:本题主要考查了抛物线的简单性质和求轨迹方程的问题.解题的关键是充分挖掘题设信息整理求得x和y的关系.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
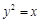 的焦点,A、B是该抛物线上的两点,
的焦点,A、B是该抛物线上的两点,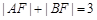 ,则线段AB的中点到y轴的距离为( )
,则线段AB的中点到y轴的距离为( )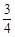 B.1 C.
B.1 C.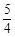 D.
D.