摘要:21.设函数.若曲线的斜率最小的切线与直线平行.求: (1)的值 (2)函数的单调区间
网址:http://m.1010jiajiao.com/timu3_id_536730[举报]
(本小题满分12分)
(理)已知函数![]() 取得极小值
取得极小值![]() .
.
(Ⅰ)求a,b的值;
(Ⅱ)设直线![]() . 若直线l与曲线S同时满足下列两个条件:
. 若直线l与曲线S同时满足下列两个条件:
(1)直线l与曲线S相切且至少有两个切点;
(2)对任意x∈R都有![]() . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
试证明:直线![]() 是曲线
是曲线![]() 的“上夹线”.
的“上夹线”.
(本小题满分12分)已知函数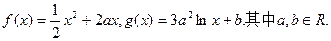
(1)设两曲线 与
与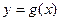 有公共点,且在公共点处的切线相同,若
有公共点,且在公共点处的切线相同,若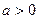 ,试建立
,试建立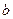 关于
关于 的函数关系式;
的函数关系式;
(2)在(1)的条件下求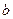 的最大值;
的最大值;
(3 )若
)若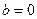 时,函数
时,函数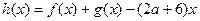 在(0,4)上为单调函数,求
在(0,4)上为单调函数,求 的取值范围。
的取值范围。
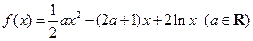 .
.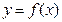 在
在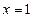 和
和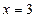 处的切线互相平行,求
处的切线互相平行,求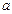 的值;
的值;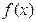 的单调区间;
的单调区间;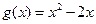 ,若对任意
,若对任意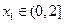 ,均存在
,均存在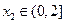 ,使得
,使得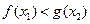 ,求
,求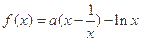
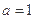 ,求曲线
,求曲线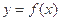 在点
在点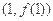 处的切线方程;
处的切线方程;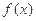 在其定义域内为增函数,求
在其定义域内为增函数,求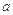 的取值范围;
的取值范围;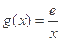 ,若在
,若在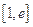 上至少存在一点
上至少存在一点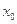 ,使得
,使得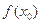
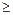
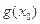 成立,求实数
成立,求实数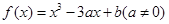 .
.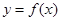 在点
在点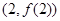 处与直线
处与直线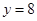 相切,求
相切,求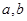 的值;
的值;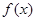 的极值点与极值.
的极值点与极值.