题目内容
(本小题满分12分)(注意:在试题卷上作答无效)
已知函数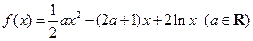 .
.
(Ⅰ)若曲线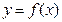 在
在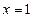 和
和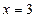 处的切线互相平行,求
处的切线互相平行,求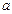 的值;
的值;
(Ⅱ)求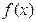 的单调区间;
的单调区间;
(Ⅲ)设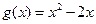 ,若对任意
,若对任意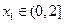 ,均存在
,均存在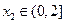 ,使得
,使得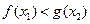 ,求
,求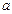 的取值范围.
的取值范围.
解:
 . ………………1分
. ………………1分
(Ⅰ)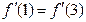 ,解得
,解得 . ………………3分
. ………………3分
(Ⅱ)
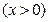 . ………………4分
. ………………4分
①当 时,
时, ,
,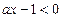 ,
,
在区间 上,
上,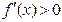 ;在区间
;在区间 上
上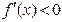 ,
,
故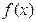 的单调递增区间是
的单调递增区间是 ,单调递减区间是
,单调递减区间是 . ………………5分
. ………………5分
②当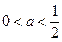 时,
时, ,
,
在区间 和
和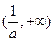 上,
上,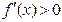 ;在区间
;在区间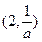 上
上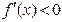 ,
,
故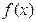 的单调递增区间是
的单调递增区间是 和
和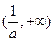 ,单调递减区间是
,单调递减区间是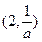 . …………6分
. …………6分
③当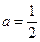 时,
时,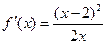 , 故
, 故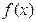 的单调递增区间是
的单调递增区间是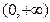 . ………7分
. ………7分
④当 时,
时,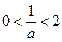 ,
,
在区间 和
和 上,
上,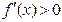 ;在区间
;在区间 上
上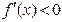 ,
,
故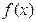 的单调递增区间是
的单调递增区间是 和
和 ,单调递减区间是
,单调递减区间是 . ………8分
. ………8分
(Ⅲ)由已知,在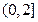 上有
上有 . ………………9分
. ………………9分
由已知,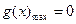 ,由(Ⅱ)可知,
,由(Ⅱ)可知,
①当 时,
时,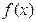 在
在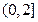 上单调递增,
上单调递增,
故 ,
,
所以,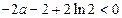 ,解得
,解得 ,故
,故 . ……………10分
. ……………10分
②当 时,
时,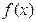 在
在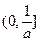 上单调递增,在
上单调递增,在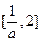 上单调递减,
上单调递减,
故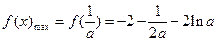 .
.
由 可知
可知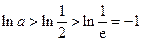 ,
, ,
,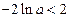 ,
,
所以,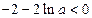 ,
,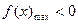 ,
,
综上所述, . &nb
. &nb
解析

练习册系列答案
相关题目