摘要:22.已知集合其中.由中的元素构成两个相应的集合..其中是有序实数对.集合的元素个数分别为.若对于任意的.则称集合具有性质. (Ⅰ)检验集合与是否具有性质.并对其中具有性质的集合写出相应的集合, (Ⅱ)对任何具有性质的集合.证明:, (Ⅲ)判断的大小关系.并证明你的结论.
网址:http://m.1010jiajiao.com/timu3_id_536446[举报]
(本小题满分12分)已知集合![]() 其中
其中![]() ,由
,由![]() 中的元素构成两个相应的集合
中的元素构成两个相应的集合![]() ,
,![]() ,其中
,其中![]() 是有序实数对,集合
是有序实数对,集合![]() 的元素个数分别为
的元素个数分别为![]() .若对于任意的
.若对于任意的![]() ,则称集合
,则称集合![]() 具有性质
具有性质![]() .
.
(Ⅰ)检验集合![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并对其中具有性质
,并对其中具有性质![]() 的集合写出相应的集合
的集合写出相应的集合![]() ;
;
(Ⅱ)对任何具有性质![]() 的集合
的集合![]() ,证明:
,证明:![]() ;
;
(Ⅲ)判断![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
已知集合 ,其中
,其中 ,由
,由 中的元素构成两个相应的集合:
中的元素构成两个相应的集合: ,
, .其中
.其中 是有序数对,集合
是有序数对,集合 和
和 中的元素个数分别为
中的元素个数分别为 和
和 .若对于任意的
.若对于任意的 ,总有
,总有 ,则称集合
,则称集合 具有性质
具有性质 .
.
(I)检验集合 与
与 是否具有性质
是否具有性质 并对其中具有性质
并对其中具有性质 的集合,写出相应的集合
的集合,写出相应的集合 和
和 ;
;
(II)对任何具有性质 的集合
的集合 ,证明:
,证明: ;
;
(III)判断 和
和 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
已知集合 ,其中
,其中 ,由
,由 中的元素构成两个相应的集合:
中的元素构成两个相应的集合:
 ,
, .
.
其中 是有序数对,集合
是有序数对,集合 和
和 中的元素个数分别为
中的元素个数分别为 和
和 .
.
若对于任意的 ,总有
,总有 ,则称集合
,则称集合 具有性质
具有性质 .
.
(I)检验集合 与
与 是否具有性质
是否具有性质 并对其中具有性质
并对其中具有性质 的集合,写出相应的集合
的集合,写出相应的集合 和
和 ;
;
(II)对任何具有性质 的集合
的集合 ,证明:
,证明: ;
;
(III)判断 和
和 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
查看习题详情和答案>>
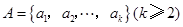 ,其中
,其中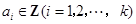 ,由
,由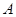 中的元素构成两个相应的集合:
中的元素构成两个相应的集合: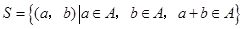 ,
,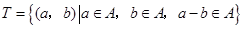 .其中
.其中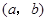 是有序数对,集合
是有序数对,集合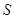 和
和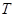 中的元素个数分别为
中的元素个数分别为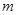 和
和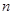 .若对于任意的
.若对于任意的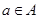 ,总有
,总有 ,则称集合
,则称集合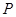 .
.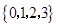 与
与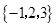 是否具有性质
是否具有性质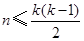 ;
;