摘要:5.设点在椭圆的长轴上.点是椭圆上任意一点. 当的模最小时.点恰好落在椭圆的右顶点.求实数的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_536103[举报]
(本题满分12分)设A(x![]() ,y
,y![]() )、B(x
)、B(x![]() ,y
,y![]() ) 是椭圆
) 是椭圆![]() (a > b > 0) 上的两点,
(a > b > 0) 上的两点,![]() ,
,![]() = (
= (![]() ,
,![]() ),且满足
),且满足![]() ·
·![]() = 0,椭圆的离心率e =
= 0,椭圆的离心率e = ![]() ,短轴长为2,O为坐标原点.(1)求椭圆的方程;(2)若存在斜率为k的直线AB过椭圆的焦点F(0,c)(c为半焦距),求直线AB的斜率k的值.
,短轴长为2,O为坐标原点.(1)求椭圆的方程;(2)若存在斜率为k的直线AB过椭圆的焦点F(0,c)(c为半焦距),求直线AB的斜率k的值.
(本题满分12分)设A(x ,y
,y )、B(x
)、B(x ,y
,y ) 是椭圆
) 是椭圆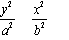 (a > b > 0) 上的两点,
(a > b > 0) 上的两点,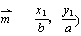 ,
,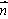 = (
= (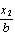 ,
,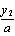 ),且满足
),且满足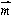 ·
·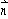 = 0,椭圆的离心率e =
= 0,椭圆的离心率e = 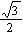 ,短轴长为2,O为坐标原点.(1)求椭圆的方程;(2)若存在斜率为k的直线AB过椭圆的焦点F(0,c)(c为半焦距),求直线AB的斜率k的值.
,短轴长为2,O为坐标原点.(1)求椭圆的方程;(2)若存在斜率为k的直线AB过椭圆的焦点F(0,c)(c为半焦距),求直线AB的斜率k的值.
 ,y
,y )、B(x
)、B(x ,y
,y ) 是椭圆
) 是椭圆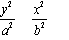 (a > b > 0) 上的两点,
(a > b > 0) 上的两点,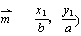 ,
,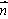 = (
= (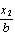 ,
,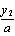 ),且满足
),且满足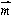 ·
·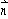 = 0,椭圆的离心率e =
= 0,椭圆的离心率e = 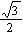 ,短轴长为2,O为坐标原点.(1)求椭圆的方程;(2)若存在斜率为k的直线AB过椭圆的焦点F(0,c)(c为半焦距),求直线AB的斜率k的值.
,短轴长为2,O为坐标原点.(1)求椭圆的方程;(2)若存在斜率为k的直线AB过椭圆的焦点F(0,c)(c为半焦距),求直线AB的斜率k的值.(本题满分12分)
已知椭圆![]() 的焦点在
的焦点在![]() 轴上,中心在原点,离心率
轴上,中心在原点,离心率![]() ,直线
,直线![]() 和以原点为圆心,椭圆
和以原点为圆心,椭圆![]() 的短半轴为半径的圆
的短半轴为半径的圆![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,点
,点![]() 是椭圆上异于
是椭圆上异于![]() 、
、![]() 的任意一点,设直线
的任意一点,设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,证明
,证明![]() 为定值;
为定值;
(Ⅲ)设椭圆方程![]() ,
,![]() 、
、![]() 为长轴两个端点,
为长轴两个端点, ![]() 为椭圆上异于
为椭圆上异于![]() 、
、![]() 的点,
的点, ![]() 、
、![]() 分别为直线
分别为直线![]() 、
、![]() 的斜率,利用上面(Ⅱ)的结论得
的斜率,利用上面(Ⅱ)的结论得![]() ( )(只需直接写出结果即可,不必写出推理过程).
( )(只需直接写出结果即可,不必写出推理过程).
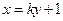 所经过的定点
所经过的定点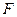 恰好是椭圆
恰好是椭圆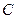 的一个焦点,且椭圆
的一个焦点,且椭圆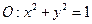 ,直线
,直线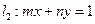 .试证明:当点
.试证明:当点 在椭圆
在椭圆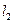 与圆
与圆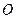 恒相交,并求直线
恒相交,并求直线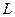 的取值范围.
的取值范围.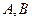 两点,若直线
两点,若直线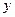 轴于点
轴于点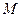 ,且
,且 ,当
,当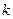 变化时,求
变化时,求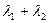 的值;
的值;