题目内容
（本题满分12分）
已知椭圆
的焦点在
轴上，中心在原点，离心率
，直线
和以原点为圆心，椭圆的短半轴为半径的圆
相切．
（Ⅰ）求椭圆的方程；
（Ⅱ）设椭圆的左、右顶点分别为
、
，点
是椭圆上异于、的任意一点，设直线
、
的斜率分别为
、
，证明
为定值；
（Ⅲ）设椭圆方程
，、为长轴两个端点， 为椭圆上异于、的点， 、分别为直线、的斜率，利用上面（Ⅱ）的结论得
（ ）（只需直接写出结果即可，不必写出推理过程）．
（Ⅰ）椭圆方程
……………4分
（Ⅱ）证明：由椭圆方程得
，
设
点坐标
则
，
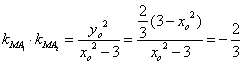
是定值 ……………10分
（Ⅲ）
……………12分
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
是首项为
，公比
的等比数列，，
，数列
.
的通项公式；（2）求数列
的前n项和Sn.
<1，xÎR }．
，求实数a的取值范围．
（
，
为常数），且方程
有两个实根为
.
的解析式；
中，四边形
是边长为
的正方形，
，
为
上的点，且
⊥平面
⊥平面
的大小；
到平面