摘要:8.点在直线上.若存在过的直线交抛物线于两点.且.则称点为“点 .那么下列结论中正确的是 A.直线上的所有点都是“点 B.直线上仅有有限个点是“点 C.直线上的所有点都不是“点 D.直线上有无穷多个点是“点 2009年普通高等学校招生全国统一考试 数 学 第Ⅱ卷
网址:http://m.1010jiajiao.com/timu3_id_534904[举报]
点![]() 在直线
在直线![]() 上,若存在过
上,若存在过![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,且
两点,且
![]() ,则称点
,则称点![]() 为“
为“![]() 点”,那么下列结论中正确的是 ( )
点”,那么下列结论中正确的是 ( )
A.直线![]() 上的所有点都是“
上的所有点都是“![]() 点”
点”
B.直线![]() 上仅有有限个点是“
上仅有有限个点是“![]() 点”
点”
C.直线![]() 上的所有点都不是“
上的所有点都不是“![]() 点”
点”
D.直线![]() 上有无穷多个点(点不是所有的点)是“
上有无穷多个点(点不是所有的点)是“![]() 点”
点”
点![]() 在直线
在直线![]() 上,若存在过
上,若存在过![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,且
两点,且![]() ,则称点
,则称点![]() 为“
为“![]() 点”,那么下列结论中正确的是 ( )
点”,那么下列结论中正确的是 ( )
A.直线![]() 上的所有点都是“
上的所有点都是“![]() 点”
点”
B.直线![]() 上仅有有限个点是“
上仅有有限个点是“![]() 点”
点”
C.直线![]() 上的所有点都不是“
上的所有点都不是“![]() 点”
点”
D.直线![]() 上有无穷多个点(点不是所有的点)是“
上有无穷多个点(点不是所有的点)是“![]() 点”
点”
![]() 点
点![]() 在直线
在直线![]() 上,若存在过
上,若存在过![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,且
两点,且![]() ,则称点
,则称点![]() 为“ 点”,那么下列结论中正确的是 ( )
为“ 点”,那么下列结论中正确的是 ( )
A.直线![]() 上的所有点都是“
上的所有点都是“![]() 点”
点”
![]() B.直线
B.直线![]() 上仅有有限个点是“
上仅有有限个点是“![]() 点”
点”
C.直线![]() 上的所有点都不是“
上的所有点都不是“![]() 点”
点” ![]()
![]()
D.直线![]() 上有无穷多个点(点不是所有的点)是“
上有无穷多个点(点不是所有的点)是“![]() 点”[来源:学。科。网]
点”[来源:学。科。网]
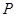 在直线
在直线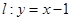 上,若存在过
上,若存在过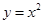 于
于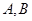 两点,且
两点,且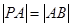 ,则称点
,则称点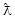 点”,那么下列结论中正确的是( )
点”,那么下列结论中正确的是( )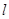 上的所有点都是“
上的所有点都是“ 在直线
在直线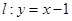 上,若存在过
上,若存在过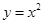 于
于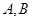 两点,且
两点,且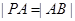 ,则称点
,则称点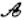 点”,那么下列结论中正确的是( )
点”,那么下列结论中正确的是( )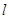 上的所有点都是“
上的所有点都是“