摘要:19. 如图.在边长为12的正方形A1 AA′A1′中.点B.C在线段AA′上.且AB = 3.BC = 4.作BB1∥AA1.分别交A1A1′.AA1′于点B1.P,作CC1∥AA1.分别交A1A1′.AA1′于点C1.Q,将该正方形沿BB1.CC1折叠.使得A′A1′ 与AA1重合.构成如图所示的三棱柱ABC-A1B1C1.在三棱柱ABC-A1B1C1中. (1)求证:AB⊥平面BCC1B1, (2)求面APQ将三棱柱ABC-A1B1C1分成上.下两部分几何体的体积之比,
网址:http://m.1010jiajiao.com/timu3_id_534893[举报]
(本题满分12分)如图,已知圆O的半径为1,点C在直径AB的延长线上,BC=1,点P是圆O上半圆上的一个动点,以PC为边作正三角形PCD,且点D
与圆心分别在PC两侧.
(1)若 ,试将四边形OPDC的面积y表示成
,试将四边形OPDC的面积y表示成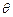 的函数;
的函数;
(2)求四边形OPDC面积的最大值.
(本题满分12分)如图,已知圆O的半径为1,点C在直径AB的延长线上,BC=1,点P是圆O上半圆上的一个动点,以PC为边作正三角形PCD,且点D
与圆心分别在PC两侧.
(1)若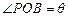 ,试将四边形OPDC的面积y表示成
,试将四边形OPDC的面积y表示成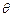 的函数;
的函数;
(2)求四边形OPDC面积的最大值.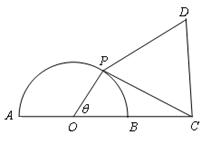
与圆心分别在PC两侧.
(1)若
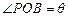 ,试将四边形OPDC的面积y表示成
,试将四边形OPDC的面积y表示成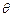 的函数;
的函数;(2)求四边形OPDC面积的最大值.

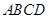 中,
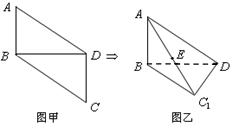
中,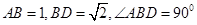 ,将它们沿对角线
,将它们沿对角线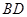 折起,折后的点
折起,折后的点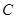 变为
变为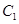 ,且
,且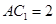 .
.
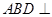 平面
平面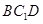 ;
;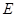 为线段
为线段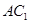 上的一个动点,当线段
上的一个动点,当线段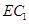 的长为多少时,
的长为多少时, 与平面
与平面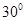 ?
? 的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=
的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA= ,M,N分别为PB,PD的中点.
,M,N分别为PB,PD的中点.
 中,
中,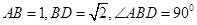 ,将它们沿对角线
,将它们沿对角线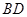 折起,折后的点
折起,折后的点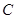 变为
变为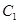 ,且
,且 .
.
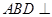 平面
平面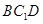 ;
;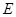 为线段
为线段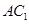 上的一个动点,当线段
上的一个动点,当线段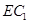 的长为多少时,
的长为多少时, 与平面
与平面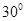 ?
?