题目内容
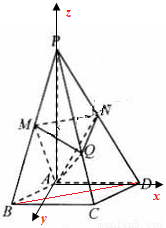
(本小题满分12分)如图,在四棱锥P—ABCD中,底面是边长为 的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=
的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA= ,M,N分别为PB,PD的中点.
,M,N分别为PB,PD的中点.

(Ⅰ)证明:MN∥平面ABCD;
(Ⅱ) 过点A作AQ⊥PC,垂足为点Q,求二面角A—MN—Q的平面角的余弦值.
【答案】
(Ⅰ)见解析;(Ⅱ)所求二面角A—MN—Q的平面角的余弦值为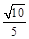 .
.
【解析】第一问在平面ABCD中找到直线BD平行于MN,利用线面平行的判定定理可以证明;第二问则借助空间向量工具,建立合适的空间坐标系,利用向量求出夹角。
解:(Ⅰ)如图连接BD.
∵M,N分别为PB,PD的中点,
∴在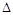 PBD中,MN∥BD.
PBD中,MN∥BD.
又MN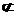 平面ABCD,
平面ABCD,
∴MN∥平面ABCD;
(Ⅱ)如图建系:
A(0,0,0),P(0,0,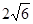 ),M(
),M(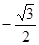 ,
, ,0),
,0),
N(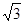 ,0,0),C(
,0,0),C(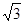 ,3,0).
,3,0).
设Q(x,y,z),则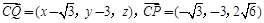 .
.
∵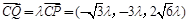 ,∴
,∴ .
.
由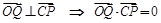 ,得:
,得: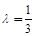 . 即:
. 即: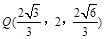 .
.
对于平面AMN:设其法向量为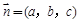 .
.
∵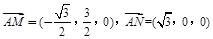 .
.
则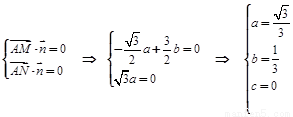 . ∴
. ∴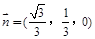 .
.
同理对于平面AMN得其法向量为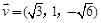 .
.
记所求二面角A—MN—Q的平面角大小为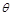 ,
,
则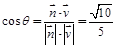 .
.
∴所求二面角A—MN—Q的平面角的余弦值为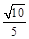 .
.

练习册系列答案
相关题目