摘要:(本题共3小题.其中第1小题4分.第2小题8分.第3小题8分.满分20分) 已知点.的坐标分别是..直线.相交于点.且它们的斜率之积为. (1)求证:点的轨迹在一个椭圆上.并写出椭圆的方程, (2)设过原点的直线交(1)中的椭圆于点..定点的坐标为.试求面积的最大值.并求此时直线的斜率, 题的解答.当的面积取得最大值时.探索(2)题的结论中直线 的斜率和所在直线的斜率之间的关系.由此推广到点位置的一般情况或椭圆的一般情况题的结论成为推广后的一个特例).试提出一个猜想或设计一个问题.尝试研究解决. [说明:本小题将根据你所提出的猜想或问题的质量分层评分]
网址:http://m.1010jiajiao.com/timu3_id_534030[举报]
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
我们把定义在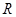 上,且满足
上,且满足 (其中常数
(其中常数 满足
满足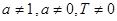 )的函数叫做似周期函数.
)的函数叫做似周期函数.
(1)若某个似周期函数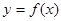 满足
满足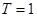 且图像关于直线
且图像关于直线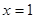 对称.求证:函数
对称.求证:函数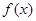 是偶函数;
是偶函数;
(2)当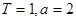 时,某个似周期函数在
时,某个似周期函数在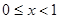 时的解析式为
时的解析式为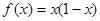 ,求函数
,求函数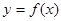 ,
,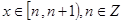 的解析式;
的解析式;
(3)对于确定的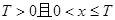 时,
时,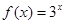 ,试研究似周期函数函数
,试研究似周期函数函数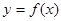 在区间
在区间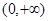 上是否可能是单调函数?若可能,求出
上是否可能是单调函数?若可能,求出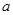 的取值范围;若不可能,请说明理由.
的取值范围;若不可能,请说明理由.
查看习题详情和答案>>
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分. 第3小题满分8分.
(理)对于数列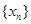 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数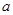 ,公比为正整数
,公比为正整数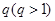 的无穷等比数列
的无穷等比数列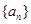 的子数列问题. 为此,他任取了其中三项
的子数列问题. 为此,他任取了其中三项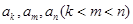 .
.
(1) 若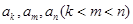 成等比数列,求
成等比数列,求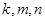 之间满足的等量关系;
之间满足的等量关系;
(2) 他猜想:“在上述数列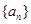 中存在一个子数列
中存在一个子数列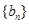 是等差数列”,为此,他研究了
是等差数列”,为此,他研究了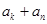 与
与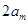 的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
(3) 他又想:在首项为正整数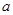 ,公差为正整数
,公差为正整数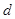 的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
查看习题详情和答案>>
(本题满分16分) 本题共有3个小题,第1小题满分4分,第2小题满分6分. 第3小题满分6分.
(理)已知椭圆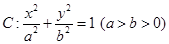 的一个焦点为
的一个焦点为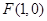 ,点
,点 在椭圆
在椭圆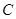 上,点
上,点 满足
满足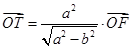 (其中
(其中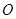 为坐标原点),过点
为坐标原点),过点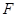 作一直线交椭圆于
作一直线交椭圆于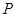 、
、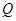 两点 .
两点 .
(1)求椭圆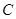 的方程;
的方程;
(2)求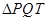 面积的最大值;
面积的最大值;
(3)设点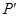 为点
为点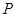 关于
关于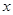 轴的对称点,判断
轴的对称点,判断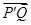 与
与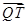 的位置关系,并说明理由.
的位置关系,并说明理由.
查看习题详情和答案>>
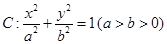 的一个焦点为
的一个焦点为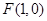 ,点
,点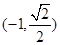 在椭圆
在椭圆 上,点
上,点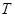 满足
满足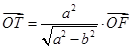 (其中
(其中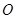 为坐标原点), 过点
为坐标原点), 过点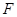 作一斜率为
作一斜率为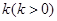 的直线交椭圆于
的直线交椭圆于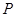 、
、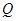 两点(其中
两点(其中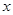 轴上方,
轴上方,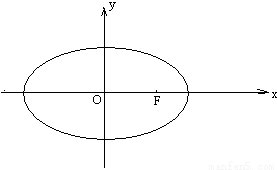
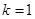 ,求
,求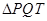 的面积;
的面积;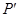 为点
为点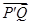 与
与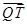 的位置关系,并说明理由.
的位置关系,并说明理由.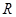 上,且满足
上,且满足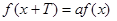 (其中常数
(其中常数 满足
满足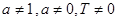 )的函数叫做似周期函数.
)的函数叫做似周期函数.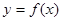 满足
满足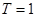 且图像关于直线
且图像关于直线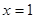 对称.求证:函数
对称.求证:函数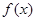 是偶函数;
是偶函数;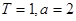 时,某个似周期函数在
时,某个似周期函数在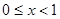 时的解析式为
时的解析式为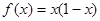 ,求函数
,求函数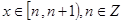 的解析式;
的解析式;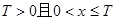 时,
时,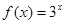 ,试研究似周期函数函数
,试研究似周期函数函数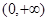 上是否可能是单调函数?若可能,求出
上是否可能是单调函数?若可能,求出 的取值范围;若不可能,请说明理由.
的取值范围;若不可能,请说明理由.