题目内容
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
我们把定义在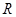 上,且满足
上,且满足 (其中常数
(其中常数 满足
满足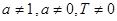 )的函数叫做似周期函数.
)的函数叫做似周期函数.
(1)若某个似周期函数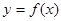 满足
满足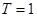 且图像关于直线
且图像关于直线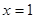 对称.求证:函数
对称.求证:函数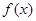 是偶函数;
是偶函数;
(2)当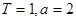 时,某个似周期函数在
时,某个似周期函数在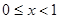 时的解析式为
时的解析式为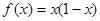 ,求函数
,求函数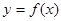 ,
,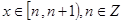 的解析式;
的解析式;
(3)对于确定的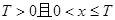 时,
时,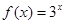 ,试研究似周期函数函数
,试研究似周期函数函数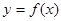 在区间
在区间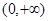 上是否可能是单调函数?若可能,求出
上是否可能是单调函数?若可能,求出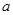 的取值范围;若不可能,请说明理由.
的取值范围;若不可能,请说明理由.
【答案】
(1)因为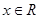 关于原点对称, 又函数
关于原点对称, 又函数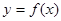 的图像关于直线
的图像关于直线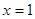 对称,所以
对称,所以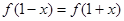 又
又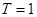 ,
,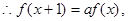 用
用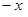 代替
代替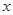 得
得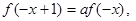 可知
可知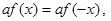
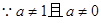 ,
,
 .即函数
.即函数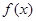 是偶函数;(2)
是偶函数;(2)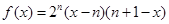 ;(3)
;(3)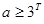 .
.
【解析】
试题分析:因为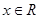 关于原点对称, 又函数
关于原点对称, 又函数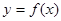 的图像关于直线
的图像关于直线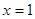 对称,
对称,
所以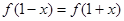 , 又
, 又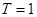 ,
,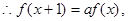 用
用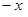 代替
代替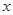 得
得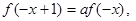 可知
可知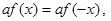
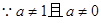 ,
,
 .即函数
.即函数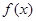 是偶函数;
是偶函数;
(2)当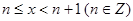 时,
时,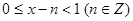
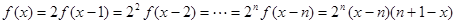 ;
;
(3)当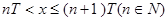 时,
时,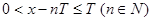
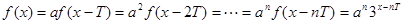
显然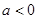 时,函数
时,函数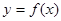 在区间
在区间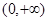 上不是单调函数
上不是单调函数
又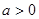 时,
时,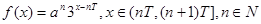 是增函数,
是增函数,
此时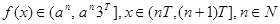
若函数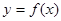 在区间
在区间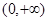 上是单调函数,那么它必须是增函数,则必有
上是单调函数,那么它必须是增函数,则必有
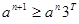 ,解得
,解得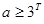 .
.
考点:本题考查了函数的性质
点评:函数的基本性质有单调性和奇偶性,它们是函数的两个重要的性质,在解决函数问题中起着非常重要的作用,主要用于判断函数单调性、求最值、求参数的取值范围等

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 和正数
和正数 ,且对任意的正整数n,当
,且对任意的正整数n,当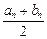 ≥0时, 有[
≥0时, 有[ ,
,  ]=
]= ,
, 
 ].
]. }是等比数列;
}是等比数列; ,求证
,求证
 ;
; ,使得数列
,使得数列 为常数数列?请说明理由
为常数数列?请说明理由 到其准线的距离等于5.
到其准线的距离等于5. 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值; 且
且 与
与 面积之和的最小值.
面积之和的最小值.
 ,对于项数为
,对于项数为 的有穷数列
的有穷数列 ,令
,令 为
为 中最大值,称数列
中最大值,称数列 为
为 3,5,4,7的创新数列为3,5,5,7.
3,5,4,7的创新数列为3,5,5,7. 的所有排列,将每种排列都视为一个有穷数列
的所有排列,将每种排列都视为一个有穷数列 .
. ,写出创新数列为3,4,4,4的所有数列
,写出创新数列为3,4,4,4的所有数列 的首项为1,前
的首项为1,前 项和为
项和为 ,且满足
,且满足 ,
, .数列
.数列 满足
满足 .
.  时,试比较
时,试比较 与
与 的大小,并说明理由;
的大小,并说明理由;
 是否可能恰为直线
是否可能恰为直线
 的方向向量?请说明你的理由.
的方向向量?请说明你的理由.