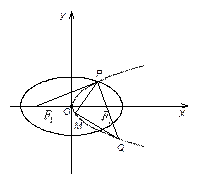
摘要:21.. 如图.设抛物线()的准线与轴交于.焦点为,以.为焦点.离心率的椭圆与抛物线在轴上方的一个交点为. (1)当时.求椭圆的方程, 的条件下.直线经过椭圆的右焦点.与抛物线交于..如果以线段为直径作圆.试判断点与圆的位置关系.并说明理由, (3)是否存在实数.使得的边长是连续的自然数.若存在.求出这样的实数,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu3_id_533818[举报]
(本小题满分14分)
如图,设抛物线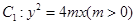 的准线与
的准线与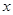 轴交于
轴交于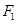 ,焦点为
,焦点为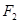 ;以
;以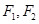 为焦点,离心率
为焦点,离心率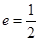 的椭圆
的椭圆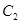 与抛物线
与抛物线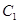 在
在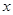 轴上方的交点为
轴上方的交点为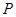 ,延长
,延长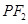 交抛物线于点
交抛物线于点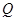 ,
,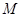 是抛物线
是抛物线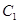 上一动点,且M在
上一动点,且M在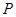 与
与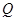 之间运动.
之间运动.
(1)当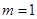 时,求椭圆
时,求椭圆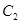 的方程,
的方程,
(2)当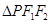 的边长恰好是三个连续的自然数时,
的边长恰好是三个连续的自然数时,
求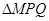 面积的最大值.
面积的最大值.

查看习题详情和答案>>
(本小题满分14分)
如图,设抛物线 的准线与
的准线与 轴交于
轴交于 ,焦点为
,焦点为 ;以
;以 为焦点,离心率
为焦点,离心率 的椭圆
的椭圆 与抛物线
与抛物线 在
在 轴上方的交点为
轴上方的交点为 ,延长
,延长 交抛物线于点
交抛物线于点 ,
, 是抛物线
是抛物线 上一动点,且M在
上一动点,且M在 与
与 之间运动.
之间运动.
(1)当 时,求椭圆
时,求椭圆 的方程,
的方程,
(2)当 的边长恰好是三个连续的自然数时,
的边长恰好是三个连续的自然数时,
求 面积的最大值.
面积的最大值.

查看习题详情和答案>>
(本小题满分14分)
如图,设抛物线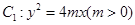 的准线与
的准线与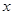 轴交于
轴交于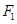 ,焦点为
,焦点为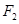 ;以
;以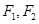 为焦点,离心率
为焦点,离心率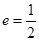 的椭圆
的椭圆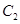 与抛物线
与抛物线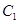 在
在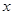 轴上方的交点为
轴上方的交点为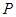 ,延长
,延长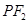 交抛物线于点
交抛物线于点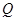 ,
,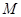 是抛物线
是抛物线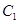 上一动点,且M在
上一动点,且M在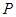 与
与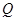 之间运动.
之间运动.
(1)当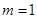 时,求椭圆
时,求椭圆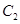 的方程,
的方程,
(2)当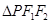 的边长恰好是三个连续的自然数时,
的边长恰好是三个连续的自然数时,
求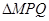 面积的最大值.
面积的最大值.

查看习题详情和答案>>
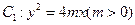 的准线与
的准线与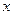 轴交于
轴交于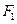 ,焦点为
,焦点为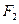 ;以
;以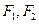 为焦点,离心率
为焦点,离心率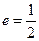 的椭圆
的椭圆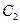 与抛物线
与抛物线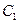 在
在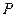 ,延长
,延长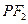 交抛物线于点
交抛物线于点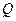 ,
,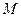 是抛物线
是抛物线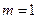 时,求椭圆
时,求椭圆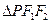 的边长恰好是三个连续的自然数时,
的边长恰好是三个连续的自然数时,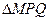 面积的最大值.
面积的最大值.