摘要:[选做题] A.选修4-1:几何证明选讲 如图.在Rt△ABC中.,BE平分∠ABC交AC于点E.点D在AB上.. (1) 求证:AC是△BDE的外接圆的切线, (2)若.求EC的长. B.选修4-2:矩阵与变换 给定矩阵A=.B =. (Ⅰ)求A的特征值.及对应特征向量. (Ⅱ)求. C.选修4-4:坐标系与参数方程 求直线 ()被曲线所截的弦长. D.选修4-5:不等式选讲 设是内的一点.是到三边的距离.是外接圆的半径.证明
网址:http://m.1010jiajiao.com/timu3_id_533168[举报]
[选做题]
A.选修4—1:几何证明选讲
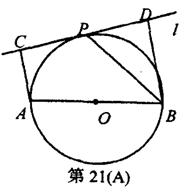
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:
(1)l是⊙O的切线;
(2)PB平分∠ABD.
|
二阶矩阵
 对应的变换将点
对应的变换将点 与
与 分别变换成点
分别变换成点 与
与 .求矩阵
.求矩阵 ;
;C.选修4—4:坐标系与参数方程
若两条曲线的极坐标方程分别为??=l与??=2cos(θ+),它们相交于A,B两点,求线
段AB的长.
D.选修4—5:不等式选讲
求函数
 的最大值.
查看习题详情和答案>>
的最大值.
查看习题详情和答案>>
[选做题]
A.选修4—1:几何证明选讲
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:
(1)l是⊙O的切线;
(2)PB平分∠ABD.

B.选修4—2:矩阵与变换
二阶矩阵 对应的变换将点
对应的变换将点 与
与 分别变换成点
分别变换成点 与
与 .求矩阵
.求矩阵 ;
;
C.选修4—4:坐标系与参数方程
若两条曲线的极坐标方程分别为=l与=2cos(θ+),它们相交于A,B两点,求线
段AB的长.
D.选修4—5:不等式选讲
求函数 的最大值.
的最大值.
查看习题详情和答案>>
[选做题]
A.选修4—1:几何证明选讲
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:
(1)l是⊙O的切线;
(2)PB平分∠ABD.
B.选修4—2:矩阵与变换
二阶矩阵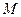 对应的变换将点
对应的变换将点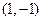 与
与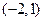 分别变换成点
分别变换成点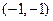 与
与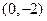 .求矩阵
.求矩阵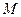 ;
;
C.选修4—4:坐标系与参数方程
若两条曲线的极坐标方程分别为??=l与??=2cos(θ+),它们相交于A,B两点,求线
段AB的长.
D.选修4—5:不等式选讲
求函数 的最大值.
的最大值.
A.选修4—1:几何证明选讲
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:
(1)l是⊙O的切线;
(2)PB平分∠ABD.

|
二阶矩阵
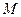 对应的变换将点
对应的变换将点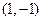 与
与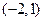 分别变换成点
分别变换成点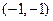 与
与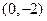 .求矩阵
.求矩阵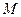 ;
;C.选修4—4:坐标系与参数方程
若两条曲线的极坐标方程分别为??=l与??=2cos(θ+),它们相交于A,B两点,求线
段AB的长.
D.选修4—5:不等式选讲
求函数
 的最大值.
的最大值.
选做题
A.选修4-1:几何证明选讲
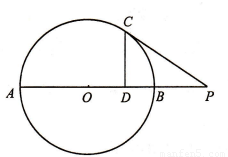
如图,自⊙O外一点P作⊙O的切线PC和割线PBA,点C为切点,割线PBA交⊙O于A,B两点,点O在AB上.作CD⊥AB,垂足为点D.
求证: .
.
B.选修4-2:矩阵与变换
设a,b∈R,若矩阵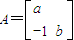 把直线l:y=2x-4变换为直线l′:y=x-12,求a,b的值.
把直线l:y=2x-4变换为直线l′:y=x-12,求a,b的值.
C.选修4-4:坐标系与参数方程
求椭圆C: =1上的点P到直线l:3x+4y+18=0的距离的最小值.
=1上的点P到直线l:3x+4y+18=0的距离的最小值.
D.选修4-5不等式选讲
已知非负实数x,y,z满足x2+y2+z2+x+2y+3z=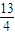 ,求x+y+z的最大值.
,求x+y+z的最大值.
 查看习题详情和答案>>
查看习题详情和答案>>
A.选修4-1:几何证明选讲
如图,自⊙O外一点P作⊙O的切线PC和割线PBA,点C为切点,割线PBA交⊙O于A,B两点,点O在AB上.作CD⊥AB,垂足为点D.
求证:
 .
.B.选修4-2:矩阵与变换
设a,b∈R,若矩阵
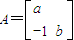 把直线l:y=2x-4变换为直线l′:y=x-12,求a,b的值.
把直线l:y=2x-4变换为直线l′:y=x-12,求a,b的值.C.选修4-4:坐标系与参数方程
求椭圆C:
 =1上的点P到直线l:3x+4y+18=0的距离的最小值.
=1上的点P到直线l:3x+4y+18=0的距离的最小值.D.选修4-5不等式选讲
已知非负实数x,y,z满足x2+y2+z2+x+2y+3z=
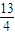 ,求x+y+z的最大值.
,求x+y+z的最大值. 查看习题详情和答案>>
查看习题详情和答案>>
 选做题(在A、B、C、D四小题中只能选做两题,并将选作标记用2B铅笔涂黑,每小题10分,共20分,请在答题指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).
选做题(在A、B、C、D四小题中只能选做两题,并将选作标记用2B铅笔涂黑,每小题10分,共20分,请在答题指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).A、(选修4-1:几何证明选讲)
如图,BD为⊙O的直径,AB=AC,AD交BC于E,求证:AB2=AE•AD
B、(选修4-2:矩形与变换)
已知a,b实数,如果矩阵M=
|
C、(选修4-4,:坐标系与参数方程)
设M、N分别是曲线ρ+2sinθ=0和ρsin(θ+
| π |
| 4 |
| ||
| 2 |
D、(选修4-5:不等式选讲)
设a,b,c是不完全相等的正数,求证:a+b+c>
| ab |
| bc |
| ca |