摘要：11．已知椭圆C:+＝1(a＞b＞0).直线l为圆O:x2+y2＝b2的一条切线.且经过椭圆的右焦点.记椭圆离心率为e． (1)若直线l的倾斜角为.求e的值, (2)是否存在这样的e.使得原点O关于直线l的对称点恰好在椭圆C上?若存在.请求出e的值,若不存在.请说明理由．
网址：http://m.1010jiajiao.com/timu3_id_532634[举报]
已知椭圆C：
＝1(a＞b＞0)，F1，F2是其左右焦点，离心率为
，且经过点(3，1)
(1)求椭圆C的标准方程；
(2)若A1、A2分别是椭圆长轴的左右端点，Q为椭圆上动点，设直线A1Q斜率为k，且k∈(－
，－
)，求直线A2Q斜率的取值范围．
已知椭圆C：
＝1(a＞b＞0)过点P(－1，－1)，c为椭圆的半焦距，且c＝
b．过点P作两条互相垂直的直线l1，l2与椭圆C分别交于另两点M，N．
（1）求椭圆C的方程；
（2）若直线l1的斜率为－1，求△PMN的面积；
（3）若线段MN的中点在x轴上，求直线MN的方程．
已知椭圆C：
＝1(a＞b＞0)的离心率为
，其左、右焦点分别是F1、F2，过点F1的直线l交椭圆C于E、G两点，且△EGF2的周长为4
.
(1)求椭圆C的方程；
(2)若过点M(2,0)的直线与椭圆C相交于两点A、B，设P为椭圆上一点，且满足
＋
＝t
(O为坐标原点)，当|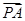
－
|＜
时，求实数t的取值范围．
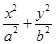＝1(a＞b＞0)的离心率为
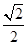，其左、右焦点分别是F1、F2，过点F1的直线l交椭圆C于E、G两点，且△EGF2的周长为4
.
＋
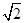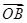＝t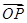
(O为坐标原点)，当|
－
|＜
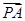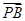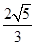时，求实数t的取值范围．
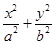＝1(a＞b＞0)过点P(－1，－1)，c为椭圆的半焦距，且c＝
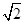b．过点P作两条互相垂直的直线l1，l2与椭圆C分别交于另两点M，N．