摘要:14.已知数列{an}的前n项和Sn是二项式展开式中含x奇次幂的系数和. 则数列{an}的通项公式an=--------.
网址:http://m.1010jiajiao.com/timu3_id_532092[举报]
已知数列{an}的前n项和Sn是二项式(1+2x)2n(n∈N*)展开式中含x奇次幂的系数和.
(1)求数列{an}的通项公式;
(2)设f(n)=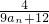 ,求cn=f(0)+f(
,求cn=f(0)+f( )+f(
)+f( )+…+f(
)+…+f(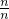 ),求
),求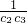 +
+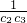 +…+
+…+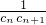 的值.
的值.
查看习题详情和答案>>
已知数列{an}的前n项和Sn是二项式(1+2x)2n(n∈N*)展开式中含x奇次幂的系数和.
(1)求数列{an}的通项公式;
(2)设f(n)=
,求cn=f(0)+f(
)+f(
)+…+f(
),求
+
+…+
的值.
查看习题详情和答案>>
(1)求数列{an}的通项公式;
(2)设f(n)=
| 4 |
| 9an+12 |
| 1 |
| n |
| 2 |
| n |
| n |
| n |
| 1 |
| c1c2 |
| 1 |
| c2c3 |
| 1 |
| cncn+1 |
已知数列{an}的前n项和Sn是二项式(1+2x)2n(n∈N* )展开式中含x奇次幂的系数和.
(1)求数列{an}的通项公式;
(2)设f(n)=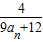 ,求f(0)+f(
,求f(0)+f(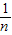 )+f(
)+f(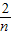 )+…+f(
)+…+f(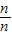 );
);
(3)证明: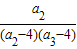 +
+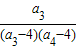 +…+
+…+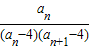 ≥
≥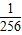 (1-
(1-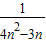 ).
).
查看习题详情和答案>>
(1)求数列{an}的通项公式;
(2)设f(n)=
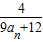 ,求f(0)+f(
,求f(0)+f(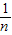 )+f(
)+f(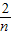 )+…+f(
)+…+f(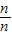 );
);(3)证明:
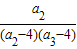 +
+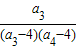 +…+
+…+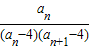 ≥
≥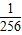 (1-
(1-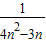 ).
).查看习题详情和答案>>
 ,求cn=f(0)+f(
,求cn=f(0)+f( )+f(
)+f( )+…+f(
)+…+f( ),求
),求 +
+ +…+
+…+ 的值.
的值.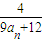 ,求f(0)+f(
,求f(0)+f(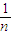 )+f(
)+f(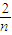 )+…+f(
)+…+f(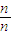 );
);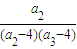 +
+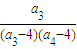 +…+
+…+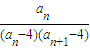 ≥
≥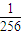 (1-
(1-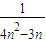 ).
).