摘要:19. 袋中共有10个大小相同的编号为1.2.3的球.其中1号球有1个.2号球有m个.3号球有n个.从袋中依次摸出2个球.已知在第一次摸出3号球的前提下.再摸出一个2号球的概率是. (Ⅰ)求m.n的值, (Ⅱ)从袋中任意摸出2个球.记得到小球的编号数之和为.求随机变量的分布列和数学期望.
网址:http://m.1010jiajiao.com/timu3_id_531970[举报]
(2012•河东区一模)袋中共有10个大小相同的编号为1、2、3的球,其中1号球有1个,2号球有m个,3号球有n个.从袋中依次摸出2个球,已知在第一次摸出3号球的前提下,再摸出一个2号球的概率是
.
(1)求m,n的值;
(2)从袋中任意摸出2个球,设得到小球的编号数之和为ξ,求随机变量ξ的分布列和 数学期望Eξ.
查看习题详情和答案>>
| 1 | 3 |
(1)求m,n的值;
(2)从袋中任意摸出2个球,设得到小球的编号数之和为ξ,求随机变量ξ的分布列和 数学期望Eξ.
袋中共有10个大小相同的编号为1,2,3的球,其中1号球有1个,2号球有m个,3号球有n个.从袋中依次摸出2个球,已知在第一次摸出3号球的前提下,再摸出一个2号球的概率是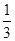 .
.
(1)求m,n的值;
(2)从袋中任意摸出2个球,设得到小球的编号数之和为ξ,求随机变量ξ的分布列.
(本小题满分12分)
袋中共有10个大小相同的编号为1、2、3的球,其中1号球有1个,2号球有m个,3号球有n个.从袋中依次摸出2个球,已知在第一次摸出3号球的前提下,再摸出一个2号球的概率是![]()
(1)求m,n的值;
(2)从袋中任意摸出2个球,设得到小球的编号数之和为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望E
的分布列和数学期望E![]() .
.
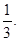
 ,求随机变量
,求随机变量 ,求随机变量
,求随机变量 .
.